1.3-二次函数的性质VIP免费

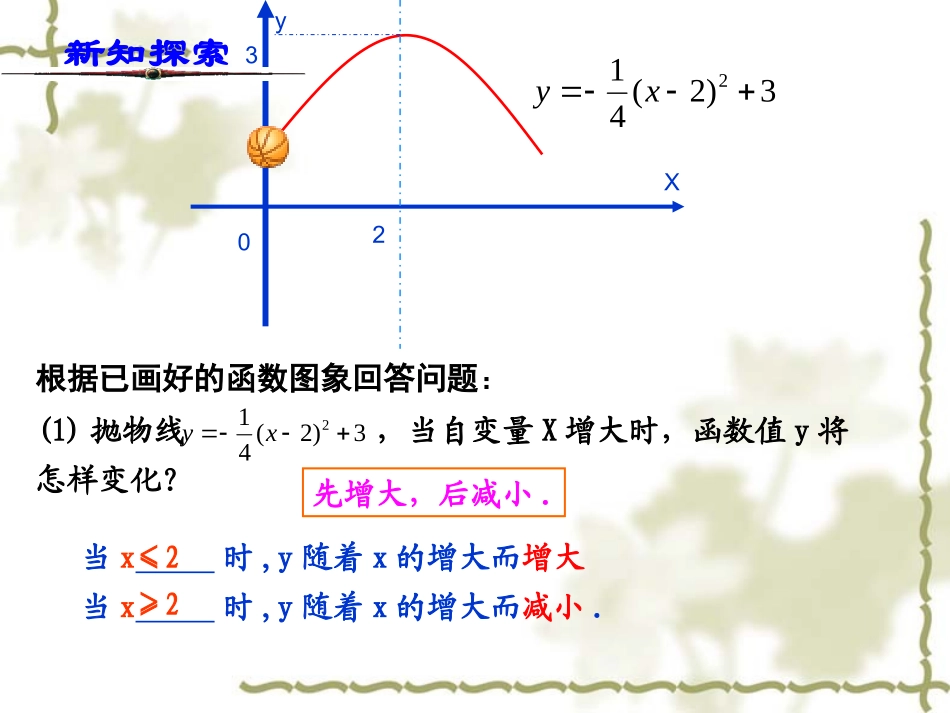
运动员投篮时，篮球运动的路线是怎样的一条曲线？2Xy033)2(412xy新知探索根据已画好的函数图象回答问题：先增大，后减小.当x时,y随着x的增大而增大当x时,y随着x的增大而减小.≤2≥2(1)抛物线，当自变量X增大时，函数值y将怎样变化？3)2(412xyXYO1122334455-1-2-3-4-5-1-2-3-4-5根据已画好的函数图象回答问题：12212xxy(2)抛物线，当自变量X增大时，函数值y将怎样变化？12212xxy先减小，后增大.当x时,y随着x的增大而减小当x时,y随着x的增大而增大.≤-2≥-2思考：二次函数的增减性由什么确定的？新知探索直线x=-23)2(412xy先增大，后减小.当x时,y随着x的增大而减小当x时,y随着x的增大而增大.≤2≥2XYO1122334455-1-2-3-4-5-1-2-3-4-5根据右边已画好的函数图象填空：12212xxy2412xxy(1)抛物线的顶点是图象的最点。12212xxy(2)抛物线的顶点是图象的最点。2412xxy该函数有没有最大值和最小值？该函数有没有最大值和最小值？当x=____时,y有最___值=______当x=____时,y有最___值=______低高-2小-12大-1思考：函数最大值或最小值由什么确定的？新知探索二次函数y=ax2+bx+c(a≠0)的图象和性质条件图象增减性最大(小)值a>0a<0XYoXYo顶点坐标a4bac4,a2b2对称轴a2bx直线顶点坐标a4bac4,a2b2对称轴a2bx直线当时，y随x的增大而减小；当时，y随x的增大而减小.当时，y随x的增大而增大.当时，y随x的增大而增大；当时，y达到最小值：a2bxabacy442无最大值.当时，y达到最大值：a2bxabacy442无最小值.新知归纳例1：已知下列函数：①求出函数对称轴和顶点坐标；②说出函数的增减性；③当x为何值时有最大值（或最小值），并求出最大值或最小值。（1）（2）3)2(22xy1532xxy新知运用新知探索二次函数y=ax2+bx+c一元二次方程ax2+bx+c=0（y=0或其他实数）（0换成y）求二次函数y=x2+2x图象与x轴的交点。解：∵与x轴的交点的纵坐标为0，∴令y=0，则x2+2x=0解得：x1=0，x2=-2；∴二次函数y=x2+2x图象与x轴有两个交点（0，0），（-2，0）则抛物线y=ax2+bx+c与x轴的两个交点坐标分别是A（），B（）x1，0x2，0xOABx1x2y抛物线y=ax2+bx+c与x轴的交点若一元二次方程ax2+bx+c=0的两个根是x1,x2，ax2+bx+c=0交点个数b2-4ac⑴y=2X２-X-1y=4X⑵2+4X+1y=3X⑶2+2X+5求抛物线与x轴的交点的个数：2个1个0个b2-4ac=(-1)2-4x2x(-1)=90﹥b2-4ac=0b2-4ac=-56<0二次函数y=ax2+bx+c的图象和x轴交点一元二次方程ax2+bx+c=0根的判别式Δ=b2-4ac有两个交点b2-4ac>0有一个交点b2-4ac=0没有交点b2-4ac<0你能画出y=2x2+3x+1这个函数的大致图象吗?结合顶点，对称轴，与y轴交点，顶点：对称轴：与y轴交点：与X轴交点：81,43直线x=431,00,210,1自变量x在什么范围内时，y随着x的增大而增大？何时y随着x的增大而减少；并求出函数的最大值或最小值。与X轴交点3.05米4米?2.25米oxy（如图），抛物线的对称轴为x=2.5。求：⑴球运动路线的函数解析式和自变量的取值范围；⑵球在运动中离地面的最大高度。解:⑴设函数解析式为:y=a(x－2.5)2+k,根据题意，得：2.52a+k=2.25(4－2.5)2a+k=3.05则：a=－0.2,k=3.5∴解析式为:y=－0.2x2+x+2.25,自变量x的取值范围为：0≤x≤4.⑵球在运动中离地面的最大高度为3.5米。篮球运动员投篮时，球运动的路线为抛物线的一部分（3）姚明双手举起的高度是2.95m,在科比前1m处，不跳起的情况，姚明能碰到科比投出的篮球吗？1（4）姚明双手举起的高度是2.95m,在科比前1m处，应跳起多少高度，姚明才能碰到科比投出的篮球吗？13.05篮球运动员投篮时，球运动的路线为抛物线的一部分（如图），抛物线的对称轴为x=2.5。求：⑴球运动路线的函数解析式和自变量的取值范围；⑵球在运动中离地面的最大高度。（3）姚明双手举起的高度是2.95m,在科比前1m处，不跳起的情况，姚明能碰到科比投出的篮球吗？（4）姚明双手举起的高度是2.95m,在科比前1m处，应跳起多少高度，姚明才能碰到科比投出的篮球吗？题目回顾总结1，抓住本质与特点2，化繁为简，化整为零，个个击破。作业：相应的配套练习。