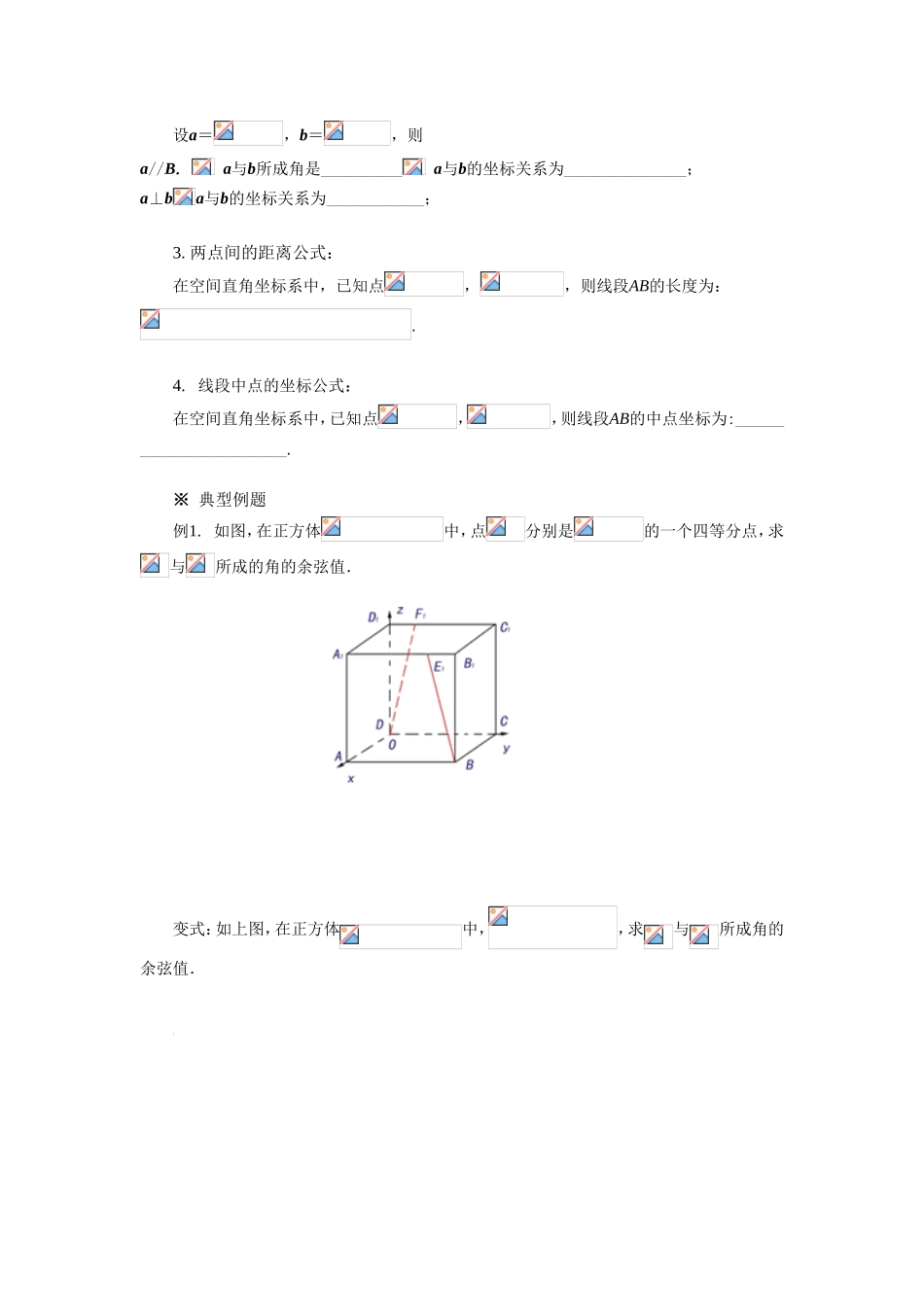
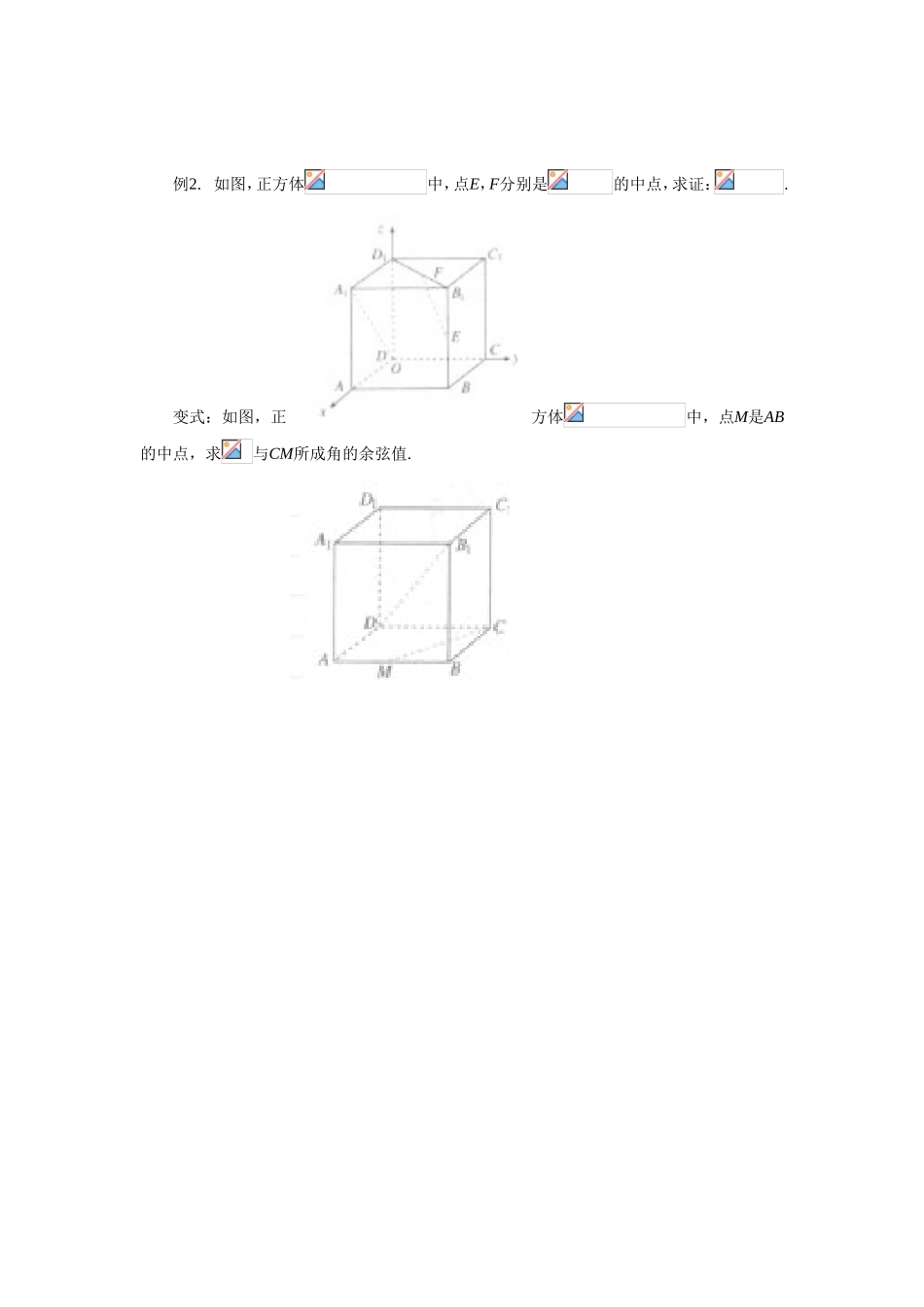
《空间向量运算的坐标表示》导学案学习目标1.掌握空间向量的长度公式、夹角公式、两点间距离公式、中点坐标公式;2.会用这些公式解决有关问题.学习重难点重点:掌握空间向量的长度公式、夹角公式、两点间距离公式、中点坐标公式;难点:会用这些公式解决有关问题.学习过程一、课前准备(预习教材P95~P97,找出疑惑之处)复习1:设在平面直角坐标系中,A,B,则线段︱AB︱=__________.复习2:已知,求:⑴a+B.⑵3a-b;⑶6A.;⑷a·b.二、新课导学※学习探究探究任务一:空间向量坐标表示夹角和距离公式问题:在空间直角坐标系中,如何用坐标求线段的长度和两个向量之间的夹角?新知:1.向量的模:设a=,则|a|=________2.两个向量的夹角公式:设a=,b=,由向量数量积定义:a·b=|a||b|cos<a,b>,又由向量数量积坐标运算公式:a·b=___________,由此可以得出:cos<a,b>=___________试试:当cos<a、b>=1时,a与b所成角是_________;当cos<a、b>=-1时,a与b所成角是________;当cos<a、b>=0时,a与b所成角是_________,即a与b的位置关系是________,用符合表示为_________.反思:设a=,b=,则a//B.a与b所成角是__________a与b的坐标关系为_______________;a⊥ba与b的坐标关系为____________;3.两点间的距离公式:在空间直角坐标系中,已知点,,则线段AB的长度为:.4.线段中点的坐标公式:在空间直角坐标系中,已知点,,则线段AB的中点坐标为:________________________.※典型例题例1.如图,在正方体中,点分别是的一个四等分点,求与所成的角的余弦值.变式:如上图,在正方体中,,求与所成角的余弦值.[例2.如图,正方体中,点E,F分别是的中点,求证:.变式:如图,正方体中,点M是AB的中点,求与CM所成角的余弦值.小结:求两个向量的夹角或角的余弦值的关键是在合适的直角坐标系中找出两个向量的坐标,然后再用公式计算.三、总结提升※学习小结1.空间向量的长度公式、夹角公式、两点间距离公式、中点坐标公式;2.解决立体几何中有关向量问题的关键是如何建立合适的空间直角坐标系,写出向量的坐标,然后再代入公式进行计算.※知识拓展在平面内取正交基底建立坐标系后,坐标平面内的任意一个向量,都可以用二元有序实数对表示,平面向量又称二维向量.空间向量可用三元有序实数组表示,空间向量又称三维向量.二维向量和三维向量统称为几何向量.学习评价※当堂检测(时量:5分钟满分:10分)计分:1.若a=,b=,则是的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不不要条件2.已知,且,则x=________.3.已知,与的夹角为120°,则的值为()A.B.C.D.4.若,且的夹角为钝角,则的取值范围是()A.B.C.D.5.已知,且,则()A.B.C.D.《空间向量及其运算》导学案学习目标1.熟练掌握空间向量的加法,减法,向量的数乘运算,向量的数量积运算及其坐标表示;2.熟练掌握空间线段的长度公式、夹角公式、两点间距离公式、中点坐标公式,并能熟练用这些公式解决有关问题.学习重难点重点:熟练掌握空间向量的加法,减法,向量的数乘运算,向量的数量积运算及其坐标表示;难点:熟练掌握空间线段的长度公式、夹角公式、两点间距离公式、中点坐标公式,并能熟练用这些公式解决有关问题.学习过程一、课前准备:(阅读课本p115)复习:1.具有_____和_____的量叫向量,________叫向量的模;______________叫零向量,记着________;_____________________具有______________________叫单位向量.2.向量的加法和减法的运算法则有_____________法则____________和__________法则.3.实数λ与向量a的积是一个量,记作________,其长度和方向规定如下:(1)|λa|=____________.(2)当λ>0时,λa与A___________;当λ<0时,λa与A_____________;当λ=0时,λa=__________.4.向量加法和数乘向量运算律:交换律:a+b=___________结合律:(a+b)+c=______________.数乘分配律:λ(a+b)=____________.5.①表示空间向量的___________所在的直线互相_______或_______,则这些向量叫共线向量,也叫平行向量.②空间向量共线定理:对空间任意两个向量(),的充要条件是存...