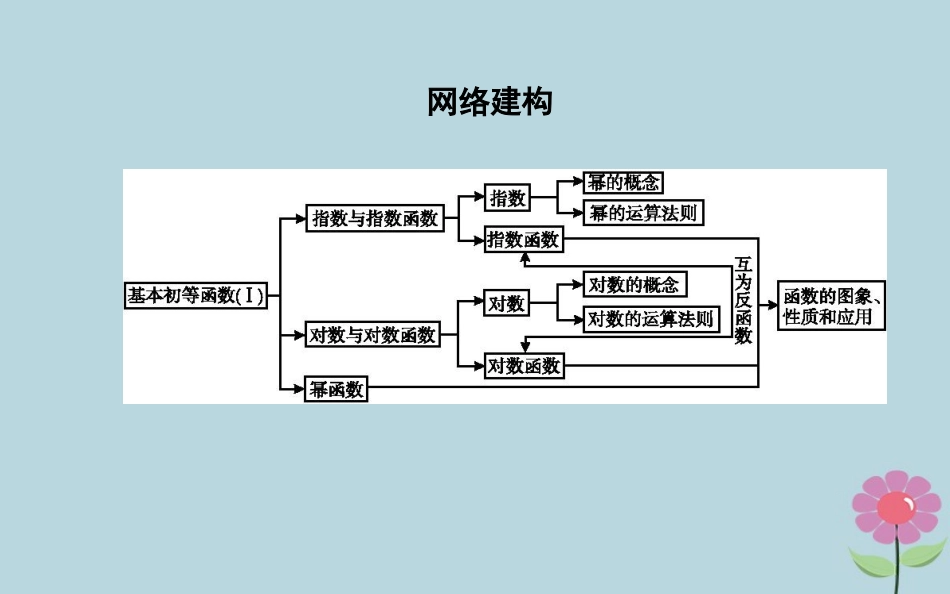
章末总结网络建构名师导学本章要解决的主要问题是:指数、对数、幂的计算和化简,指数函数、对数函数、幂函数的概念、图象、性质及应用.解决上述问题的关键是:理解并掌握好幂函数、指数函数、对数函数的运算,指数函数、对数函数、幂函数的概念、性质和图象等基础知识,做到基础知识无盲点.要注意函数与方程思想的应用,进一步形成应用函数思想、数形结合思想解决问题的能力.题型探究·素养提升类型一幂、指、对数的运算思路点拨:利用指数幂、对数的运算法则及性质进行化简或计算,要注意法则的正、逆应用.(1)(0.000114)+2237-124964+1.519;解:(1)原式=(0.1414)+(3323)-12278+32213=0.1-1+32-178+313=10+9-87+27=3147.解:(2)原式=22log23+23log3-2log(2)4=32+12-4=-2.(2)log48-19log3-2log4.方法技巧(1)指数幂的运算关键是化负指数为正指数,化根式为分数指数幂,化小数为分数.(2)对数式的化简或计算要注意利用对数的运算性质或对数恒等式、换底公式来进行.类型二比较大小问题【例2】(1)(2017·天津卷)已知奇函数f(x)在R上是增函数.若a=-f(log215),b=f(log24.1),c=f(20.8),则a,b,c的大小关系为()(A)a
log24.1>log24=2>20.8,所以f(log25)>f(log24.1)>f(20.8),所以a>b>c.故选C.(2)设a>b>1,c<0,给出下列三个结论:①ca>cb;②acloga(b-c).其中所有的正确结论的序号是()(A)①(B)①②(C)②③(D)①②③解析:(2)由a>b>1可得0<1a<1b,故ca>cb,①正确;结合指数函数性质,a>b>1时,若c<0则acb-c>1,故logb(a-c)>loga(a-c)>loga(b-c),③正确.故选D.方法技巧将两个需要比较大小的实数看成某类函数的函数值,利用函数的单调性比较是常用的一种方法,当两个幂形式的数的底数与指数都不同时,常利用选取中间量法进行比较.另外,还可以借助于图象法,比较(作差、作商)法等.类型三幂、指数、对数函数的性质、图象【例3】方程a-x=logax(a>0且a≠1)的实数解个数为()(A)0(B)1(C)2(D)3解析:利用数形结合法画出y2=a-x与y1=logax的图象,观察判断.当a>1时,在同一坐标系中画出y1=logax的图象和y2=a-x的图象如图(1),由图象知两函数图象只有一个交点;同理,当01时,1-x<0,故0<31-x<1.由此可得-2<31-x-2<-1.故所求函数的值域为(-2,-1].【例4】求函数f(x)=1132,1,32,1xxxx的值域.方法技巧指数函数、对数函数的性质主要是指两种函数的定义域、值域、单调性等,其中单调性是高考考查的重点,并且经常以复合函数的形式考查,求解此类问题时,要以基本函数的单调性为主,结合复合函数单调性判断法则,在函数定义域限制之下讨论.类型五函数中的思想方法思路点拨:原方程等价于13,,13.xxaxxax方程(x-1)(3-x)=a-x的解满足1134,或a≤1时,函数图象无交点,原方程无实数解.当a=134,或1