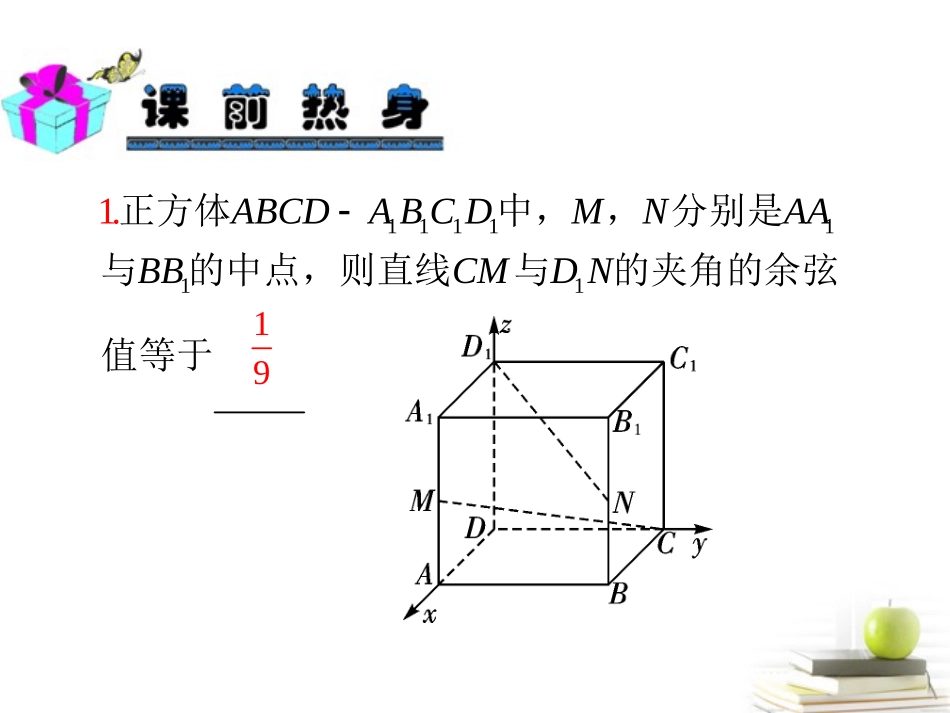
1911111111.ABCDABCDMNAABBCMDN正方体中,,分别是与的中点,则直线与的夹角的余弦值等于11111120,2,02,0,10,0,22,2,1(22,1)(2,21)1cos91.9CMDNCMDNCMDNCMDNCMDNCMDN����建立如图所示的空间直角坐标系,设正方体的棱长为,则点,,,,所以向量,,,,所以〈,〉,所以异面直线与的夹角的余弦值等于解析:22(1,2)(1)||2.AnnnBnnAB�若点,,,,,则的最小值为22222||121126()||22ABnnnnAB��解因为,所以的最小值为析:10511111111423.ABCDABCDABBCCCBCDBBD已知长方体中,,,则直线和平面所成角的正弦值为1111111114,0,04,4,04,4,24,4,00,4,2cos1610.51641616BCCACBBDDACBBDDBCBCACBCACBCAC�����如图建立空间直角坐标系,则,,,显然平面,所以为平面的一个法向解量.又,所以〈,〉析:231111114.ABCDABCDEBBAEDABCD在正方体中,点为的中点,则平面与平面所成的锐二面角的余弦值为11111.0,0,1(1,0)0,1,01(0,11)(1,0)2(1)AAEDADAEDnyz�为原点建系,设棱长为则,,,,所以,,,,设平面的法向量为,解,析:121202.121021,2,20,0,122cos.3132.3yzyzzABCD则,所以所以,因为平面的一个法向量为.所以〈,〉即所成的锐二面角的余弦值为nnnn61111425.ABCDCGABCDCGEFABADCGEF已知正方形的边长为,平面,,,分别是,的中点,则点到平面的距离为0,0,21,1,366111111CxyzOGGEFCGEFOGd��建立如图所示的空间直角坐标系,则.由题意易得平面的一个法向量.所以点到平面:距解析的离为nnn异面直线所成的角111111—21.ABCABCABBBABCB在正三棱柱中,,求与所成角【】的大小例111111111116261(0)(22221)(021)26262(1)(1)22220.90.ABBBBCABBCABBCABBCABCB��以为原点,建立如图所示空间直角坐标系.取=,则,,,,,,,,,所以=,,,,,,所以,则所以与所成角的大小是【解析】用向量法求异面直线所成的角的关键是构造直线的方向向量,利用向量的数量积进行计算.长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,E,H分别是A1B1和BB1的中点.求:(1)异面直线EH与AD1所成的角的余弦值;(2)异面直线AC1与B1C所成的角的余弦值.【变式练习1】11112,0,02,2,00,2,00,0,110,2,12,1,1(2,2)2,2,12DADCDDxyzABCDCEHB分别以、、所在直线为、、轴建立空间直角坐标系.则,,,,,析,,:,解,1111111111(01)2,0,1||||522,2,12,0,1||3||5.112112cos.55521.5HEADHEADACCBACCBHEADHEADEHAD����所以,,,,,,,,,因为,所以〈,〉所以异面直线与所成的角的余弦值为11114152cos||5355.5ACCBACBC�因为〈,〉,所以异面直线与所成的角的余弦值为直线与平面所成的角—.223.2.SABCDABCDSBCABCDABCABBCSASBSABCSDSAB45212四棱锥中,底面为平行四边形,侧面底面已知,,,证明:;求直线与平面所成【】角的正弦值例解析:(1)证明:作SO⊥BC,垂足为O,连结AO.由侧面SBC⊥底面ABCD,得SO⊥平面ABCD.因为SA=SB,所以AO=BO.又∠ABC=45°,所以△AOB为等腰直角三角形所以AO⊥OB.如图,以O为坐标原点,OA为x轴正向,建立直角坐标系O—xyz.(20,0)(020)(00)0,0,1(201)(0,20)0.ABCSSACBSACBSABC��则,,,,,,,,,,,,,.所以,所以222(0)22221()44222122()(1)(220)4422200.ABEESESEGOGGOGOGSEABOGOGSABSEABOGSABOGDSSDS���取的中点,则,,,连接,取的中点,连接,则,,.故,,,,,,,,,所以,,所以与平面内两条相交直线、垂直,所以平面与的夹角记为,与平面AB所成的角记为,则与互余.(2220)(2221)cos22122212244211111222sin1122.11DOGDSDSOGDSSDSAB���因为,,,所以,,,所以,则所以,直线与平面所成的角的正...