高中数学 双曲线几何意义课件 新人教A版选修2-1 课件VIP免费

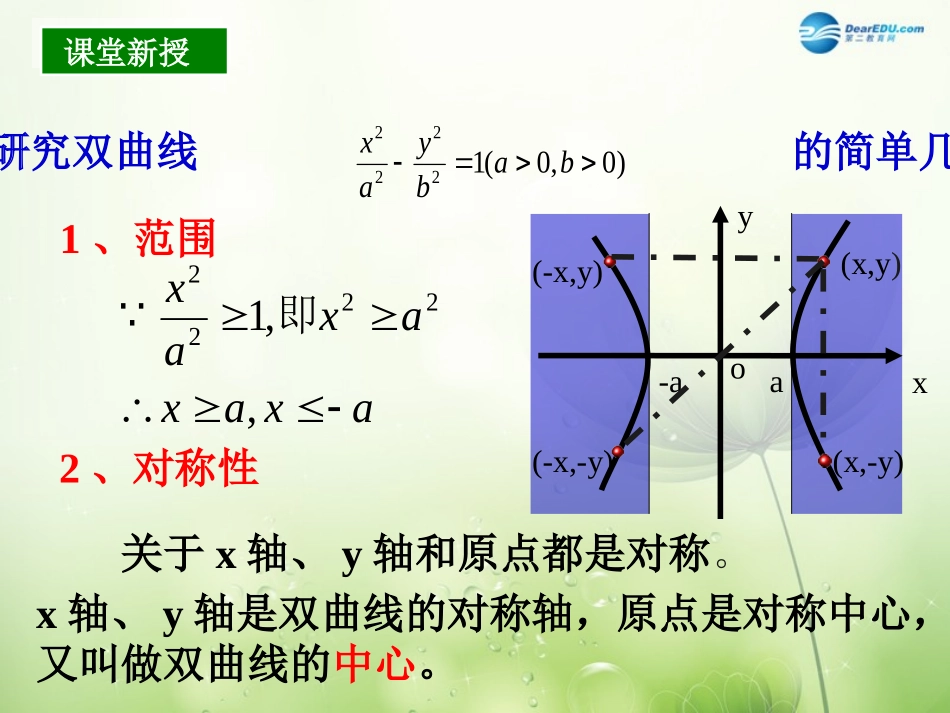
8.48.4双曲线的简单双曲线的简单几何性质几何性质双曲线的标准方程形式一：（焦点在x轴上，（-c，0）、（c，0））)0,0(12222babyax1F2F形式二：（焦点在y轴上，（0，-c）、（0，c））其中)0,0(12222babxay1F2F222cba复习复习2、对称性一、研究双曲线的简单几何性质)0,0(12222babyax1、范围axaxaxax,,12222即关于x轴、y轴和原点都是对称。x轴、y轴是双曲线的对称轴，原点是对称中心，又叫做双曲线的中心。xyo-aa(-x,-y)(-x,y)(x,y)(x,-y)课堂新授课堂新授3、顶点（1）双曲线与对称轴的交点，叫做双曲线的顶点xyo-b1B2Bb1A2A-aa)0,()0,(21aAaA、顶点是如图，线段叫做双曲线的实轴，它的长为2a,a叫做实半轴长；线段叫做双曲线的虚轴，它的长为2b,b叫做双曲线的虚半轴长2A1A2B1B（2）实轴与虚轴等长的双曲线叫等轴双曲线（3）)0(22mmyxM(x,y)4、渐近线1A2A1B2BN(x,y’)Q:的位置关系它与xaby:的位置的变化趋势它与xaby的下方在xaby慢慢靠近xyoxabyxabyab)0(22xaxaby分的方程为双曲线在第一象限内部xabybabyax的渐近线为双曲线)0,0(12222（1）的渐近线为等轴双曲线)0(22mmyx（2）xy利用渐近线可以较准确的画出双曲线的草图（3）5、离心率双曲线的叫做的比双曲线的焦距与实轴长,ace离心率。c>a>0e>1e是表示双曲线开口大小的一个量,e越大开口越大（1）定义：（2）e的范围：（3）e的含义：11)(2222eacaacab也增大增大且时，当abeabe,),,0(),1(的夹角增大增大时，渐近线与实轴eace222bac二四个参数中，知二可求、、、在ecba（4）等轴双曲线的离心率e=?2(5)的双曲线是等轴双曲线离心率2exyo的简单几何性质二、导出双曲线)0,0(12222babxay-aab-b（1）范围:ayay,（2）对称性:关于x轴、y轴、原点都对称（3）顶点:(0,-a)、(0,a)（4）渐近线:xbay（5）离心率:ace小结(比较异同）小结(比较异同）xyoax或axayay或)0,(a),0(axabyxbayace)(222bac其中关于坐标轴和原点都对称性质双曲线)0,0(12222babyax)0,0(12222babxay范围对称性顶点渐近线离心率图象xyo例1:求双曲线的实半轴长,虚半轴长,焦点坐标,离心率.渐近线方程。例题讲解例题讲解22916144yx.4516线和焦点坐标程，并且求出它的渐近出双曲线的方轴上，中心在原点，写焦点在，，离心率离是已知双曲线顶点间的距xe例23.求顶点在x轴上,两顶点间的距离为8,离心率e=5/4的双曲线的标准方程.12byax222（a＞b＞0）12222byax(a＞0b＞0)222ba(a＞0b＞0)c222ba(a＞b＞0)c椭圆双曲线方程abc关系图象yXF10F2MXY0F1F2p小结小结渐近线离心率顶点对称性范围准线|x|a,|y|≤b|x|≥a，yR对称轴：x轴，y轴对称中心：原点对称轴：x轴，y轴对称中心：原点（-a,0)(a,0)(0,b)(0,-b)长轴：2a短轴：2b(-a,0)(a,0)实轴：2a虚轴：2be=ac(0＜e＜1)ace=(e1)无y=abx±cax2cax2例2、双曲线型自然通风塔的外形，是双曲线的一部分绕其虚轴旋转所成的曲面，它的最小半径为12m,上口半径为13m,下口半径为25m,高55m.选择适当的坐标系，求出此双曲线的方程(精确到1m).A′A0xC′CB′By131225例题讲解例题讲解例3、点M（x,y）与定点F（c,0），的距离和它到定直线：x=的距离的比是常数（c>a>0）,求点M的轨迹.lca2acxxy0OxyF′FMl'll/ld的两条准线曲线是双1:22222byaxcaxl);3,5(,211Me经过点）离心率（、求双曲线的标准方程12122mymx、避免讨论，设为解解。轴双曲线，只有一种有、避免讨论，设两种等解.11616)1(1322222222yxmymxayax解为或、分析题意，设为解课堂练习2课堂练习2），经过点（渐近线的方程是129,32)2(xy1818),0(23)2).0(944912222222222yxyxxxyyx再代点。可得轴上，设为根据渐近线知道焦点在或为）不讨论，可以设方程解题要点：注：“共渐近线”的双曲线的应用。，为参数，程为共渐近线的双曲线系方与)0(122222222byaxbyaxλ>0表示焦点在x...