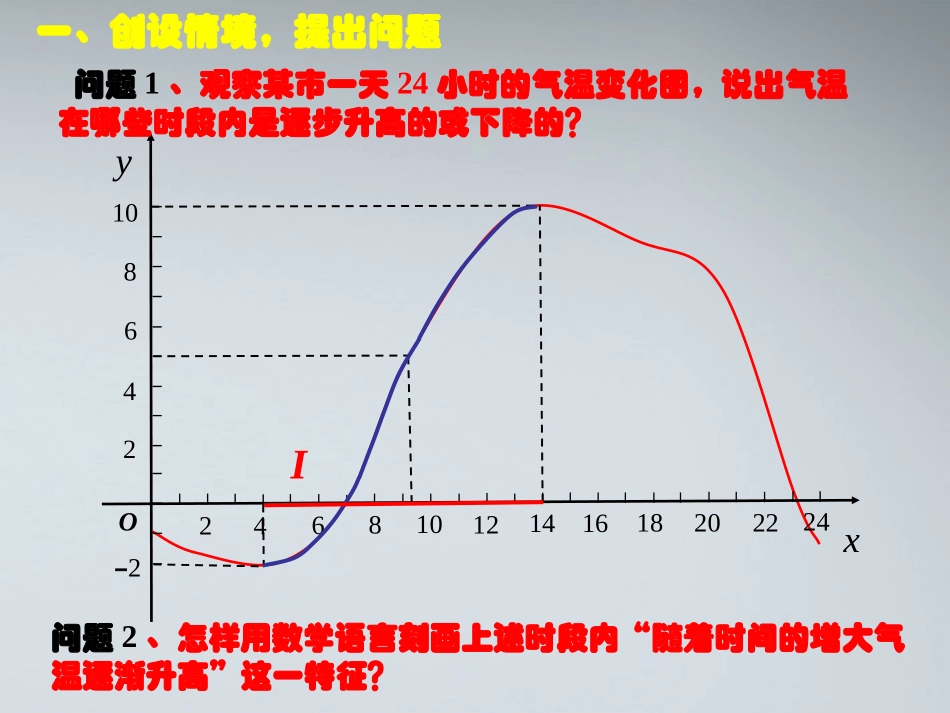
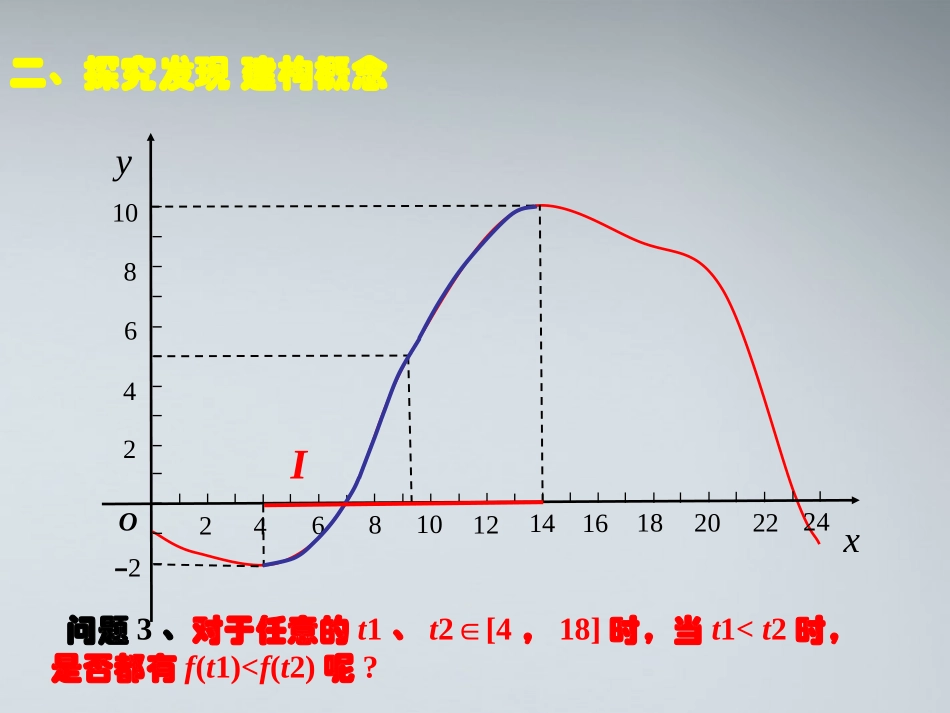
y246810O-2x84121620246210141822I问题1、观察某市一天24小时的气温变化图,说出气温在哪些时段内是逐步升高的或下降的?问题2、怎样用数学语言刻画上述时段内“随着时间的增大气温逐渐升高”这一特征?一、创设情境,提出问题y246810O-2x84121620246210141822I问题3、对于任意的t1、t2[4∈,18]时,当t1单调区间(2)函数单调性是针对某个区间而言的,是一个局部性质;(1)如果函数y=f(x)在区间I是单调增函数或单调减函数,那么就说函数y=f(x)在区间I上具有单调性。在单调区间上,增函数的图象是上升的,减函数的图象是下降的。判断1:函数f(x)=x2在是单调增函数;,xyo2yx(2)函数单调性是针对某个区间而言的,是一个局部性质;(1)如果函数y=f(x)在区间I是单调增函数或单调减函数,那么就说函数y=f(x)在区间I上具有单调性。在单调区间上,增函数的图象是上升的,减函数的图象是下降的。判断2:定义在R上的函数f(x)满足f(2)>f(1),则函数f(x)在R上是增函数;(3)x1,x2取值的任意性yxO12f(1)f(2)y246810O-2x84121620246210141822I问题6、类似气温图,你还能举出生活中的一些例子吗?问题7、你能说出你学过的函数的单调区间吗?请举例说明三、自我尝试运用概念问题5、你能找出气温图中的单调区间吗?例1、下图为函数,的图像,指出它的单调区间。[4,7]xy=fx123-2-3-2-11234567xo-4-1y-1.5[-1.5,3],[5,6][-4,-1.5],[3,5],[6,7]解:单调增区间为单调减区间为例2.画出下列函数图像,并写出单调区间:1(1)(0);yxxx1yxy1yx的单调减区间是_____________(,0)(0,),讨论1:根据函数单调性的定义,1(0)(,0)(0,)yxx能不能说在定义域上是单调减函数?2试讨论在和上的单调性?()(0)kfxkx0,,0?变式2:讨论的单调性2(0)yaxbxca成果交流变式1:讨论的单调性2(0)yaxa2(2)2.yxxyy=-x2+21-1122-1-2-22yx+2的单调增区间是_______;(,0]2yx+2的单调减区间是_______.[0,)例2.画出下列函数图像,并写出单调区间:例3、证明函数在区间上是单调增函数1yxx0,1.任取x1,x2∈D,且x1