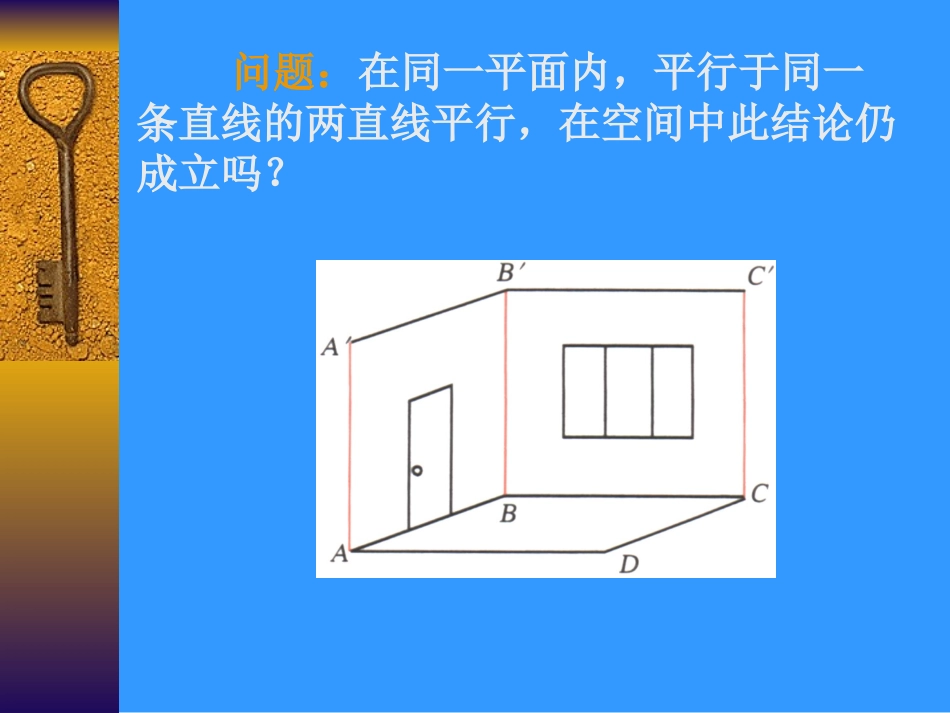
判断下列命题对错:1、如果一条直线上有一个点在一个平面上,则这条直线上的所有点都在这个平面内。()2、将书的一角接触课桌面,这时书所在平面和课桌所在平面只有一个公共点。()3、四个点中如果有三个点在同一条直线上,那么这四个点必在同一个平面内。()4、一条直线和一个点可以确定一个平面。()5、如果一条直线和另两条直线都相交,那么这三条直线可以确定一个平面。()一、复习回顾:问题:在同一平面内,平行于同一条直线的两直线平行,在空间中此结论仍成立吗?若ab∥,bc∥,caabcaα则ac∥。公理4平行于同一条直线的两条直线互相平行.公理4的特性,通常叫做空间平行线的传递性.二、新授:1、空间平行关系的传递性:平行于同一条直线的两条直线互相平行条件:结论:两条直线平行于同一条直线两条直线互相平行作用:判断两直线平行的重要依据应用之关键:找媒介(中间直线)公理4:例1.在一块长方体形状木块的面AC上有一点P,过点P画一条直线和棱C1D1平行,说明应该怎么画解:如图(1),过点P作直线MNCD∥,分别交AD,BC于M、N,则由公理4得,MNC∥1D1.图(1)DCABA1B1D1C1PMN练习:2.如图(2),在正方体ABCD-A1B1C1D1中AE=A1E1,AF=A1F1,则EF_________E1F1.平行且等于DCBAF1C1B1FEA1D1E1图22、等角定理定理:不在同一平面内的两个角,如果其中一个角的两边与另一个角的两边分别平行并且方向相同,那么这两个角相等。BACCAB和的边例2、已知:,//BAABCAAC//并且方向相同(即向量AB,BA与ACCA与的方向相同).CABBAC求证:推论:如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等.注:对于平面图形得出的结论,有些可以推广到立体图形(用公理或定理的形式给出);一般情况下,要把关于平面图形的结论推广到立体图形,必须经过证明!例3:在正方体ABCD—A1B1C1D1中,直线AB与C1D1,AD1与BC1是什么位置关系?为什么?解:C1ABCDA1B1D11)∵ABA∥1B1,C1D1A∥1B1,∴ABC∥1D12)∵ABC∥1D1,且AB=C1D1∴ABC1D1为平行四边形故AD1BC∥1练习:在上例中,AA1与CC1,AC与A1C1的位置是什么关系?例4已知ABCD是四个顶点不在同一个平面内的空间四边形,E,F,G,H分别是AB,BC,CD,DA的中点,连结EF,FG,GH,HE,求证EFGH是一个平行四边形。分析:EFGH是一个平行四边形EHFG∥且EH=FGEHBD∥且EH=BDFGBD∥且FG=BD2121连结BD,E,F,G,H分别是各边中点ABDEFGHC例4已知ABCD是四个顶点不在同一个平面内的空间四边形,E,F,G,H分别是AB,BC,CD,DA的中点,连结EF,FG,GH,HE,求证EFGH是一个平行四边形。ABDEFGHC∵EH是△ABD的中位线∴EHBD∥且EH=BD同理,FGBD∥且FG=BD∴EHFG∥且EH=FG∴EFGH是一个平行四边形证明:连结BD2121解题思想:把所要解的立体几何问题转化为平面几何的问题.——解立体几何时最主要、最常用的一种方法。变形已知四边形ABCD是空间四边形,E、H分别是边AB、AD的中点,,32CDCGCBCFF,G分别是边CB,CD上的点,且求证:四边形EFGH有一组对边平行但不相等.例5、如图,已知F、E是正方体的棱AD、的中点,求证:11DA11FCBBEC1.空间两直线平行是指它们()A.无交点B.共面且无交点C.和同一条直线垂直D.以上都不对三、练习:2.在空间,如果一个角的两边与另一个角的两边分别平行,则这两个角()A.相等B.互补C.相等或互补D.既不相等也不互补BC3.课本P11No.1四、课堂小结:1、公理4——判定空间两条直线平行的依据.(空间平行关系的传递性)2、等角定理——判定空间两个角相等的依据.(注意方向的判定)①对应向量方向全相同——两角相等;②对应向量方向全相反——两角相等;③对应向量方向一同一反——两角互补.五、作业布置:1、课本P12练习No.2、3;2、课本P14习题9.2No.1(2)、(4);No.2(1);No.6(2).