高中数学：(双曲线及标准方程)课件高二旧人教版 课件VIP免费

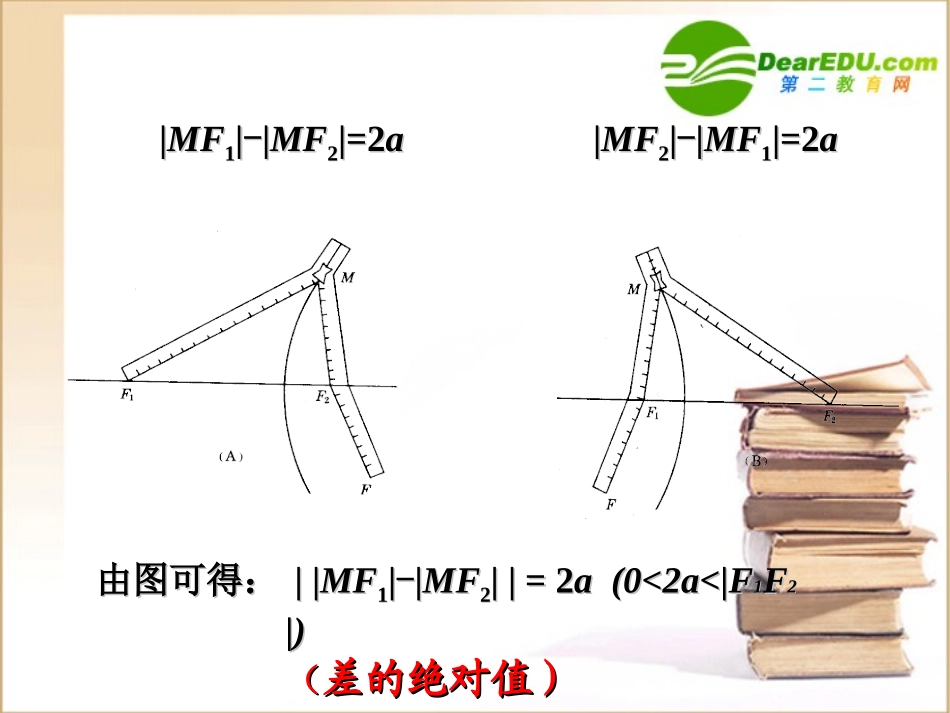
双曲线及其标准方程1.什么叫做椭圆？2a两定点F1、F2(|F1F2|=2c)和的距离的等于常数(2a>|F1F2|=2c>0)的点的轨迹.平面内与1F2F0,c0,cXYOyxM,引入问题：两定点F1、F2差的距离的等于常数的点的轨迹是什么呢？平面内与||MFMF11||--||MFMF22|=2|=2aa||MFMF22||--||MFMF11|=2|=2aa由图可得：由图可得：||||MFMF11||--||MFMF22||=2||=2a(0<2a<|Fa(0<2a<|F11FF22|)|)（（差的绝对值）差的绝对值）MM点运动时，点运动时，MM点满足什么条件？点满足什么条件？∵∵|MF|MF11|=|MF|=|MF|=|MF|=|MF22|+|F|+|F22F|F|①①如图如图(A)(A)，当，当|MF|MF11|>|MF|>|MF22||时时∴∴|MF|MF11||--|MF|MF22|=|F|=|F22F|=2F|=2aa②②如图如图(B)(B)，当，当|MF|MF11|<|MF|<|MF22||时时同理可得：同理可得：|MF|MF22||--|MF|MF11|=2|=2aa上面两条合起来叫做双曲线上面两条合起来叫做双曲线另思考：当另思考：当|MF|MF11|=|MF|=|MF22||时，时，MM点的轨迹是什么？点的轨迹是什么？由①②可得：由①②可得：||MF||MF11||--|MF|MF22||=2||=2aa（（差的绝对值）差的绝对值）其中两个定点F1、F2叫做双曲线的焦点|F1F2|=2c叫做焦距平面内与F1、F2的距离的___________为____________________的点M的轨迹两定点差的绝对值常数2a注意：在双曲线定义中必须有条件.2c>2ayxoF2F1M叫做叫做双曲线双曲线。。((小于小于|F|F11FF22|)|)4）当0＜a＜c时，动点M的轨迹是什么？(动点M的轨迹是分别以点F1、F2为端点，方向指向F1F2外侧的两条射线．)(动点M的轨迹不存在.)2）当a＞c＞0时，动点M的轨迹是什么？1）当a=c时，动点M的轨迹是什么？3）若常数a=0,轨迹是什么?(线段F1F2的垂直平分线)提出问题：(双曲线)xyo设M（x,y）,双曲线的焦距为2c（c>0）,F1(-c,0),F2(c,0)常数=2aF1F2M即(x+c)2+y2-(x-c)2+y2=+2a_以F1,F2所在的直线为X轴，线段F1F2的中点为原点建立直角坐标系1.建系.2.设点．3.列式．|MF1|-|MF2|=2a4.化简.aycxycx2)()(2222222222)(2)(ycxaycx222)(ycxaacx)()(22222222acayaxac222bac)0,0(12222babyax叫做双曲线的标准方程(焦点落在X轴上)焦点在y轴上的双曲线的标准方程是：?想一想12222bxayxyF2F1M怎样判断双曲线的焦点位置?当项的系数为正时，焦点落在x轴上当项的系数为正时，焦点落在y轴上反之也成立。2x2y222bac定义定义图象图象方程方程焦点焦点a.b.ca.b.c的关的关系系||MF1|-|MF2||=2a（2a<|F1F2|）F(±c,0)F(0,±c)12222byax12222bxayyxoF2F1MxyF2F1M归纳思考：124)2(22yx3649)4(22yx122)3(22yx124)1(22yx判断下列方程是否是双曲线的方程，如果是，判断其焦点位置，并求出三量的值。cba,,例１:已知双曲线的焦点为F1(-5,0),F2(5,0)，双曲线上一点M到F1、F2的距离的差的绝对值等于6，求双曲线的标准方程.变式:去掉“绝对值”？F2F1Mxy0解：依题意，设所求标准方程为116922yx12222byax)00(ba，则其标准方程为得由5,3ca1635222b课例分析例2一炮弹在某处爆炸，在A处听到爆炸声的时间比在B处晚2s．(1)爆炸点应在什么样的曲线上？(2)已知A、B两地相距800m，并且此时声速为340m／s，求曲线的方程．分析：(1)如图所示:设点P为爆炸点,A与B为定点,由题意可知,|PA|比|PB|长2S,即680m／s,而|AB|=800m,所以爆炸点应该在双曲线上,其中A与B为焦点.ABP●●●(2)解答过程44400222acb所求双曲线的方程为14440011560022yx400,340ca)0(xxy0ABP(x,y)-252534022||||aPBPA怎样才能找出具体爆炸点?1322yx9322yx求与圆和圆都外切的圆的圆心M的轨迹程．:2C:1C①思考题的焦点，是双曲线169x,2221yFF的直线过1F，交双曲线的左支于A,10||AB且的周长。求2ABF②F2F1MxOyBAx1C2C0yM,两点B椭圆双曲线定义图象方程a.b.c的关系|MF1|+|MF2|=2a||MF1|－|MF2||=2a22221(0)xyabab22221(0,0)xyababa>b>0，a2=b2+c2c2=a2+b2双曲线与椭圆之间的区别与联系（-c，0）yx01F2FM（c，0）（-c，0）xy01F2FM（c，0）小结: