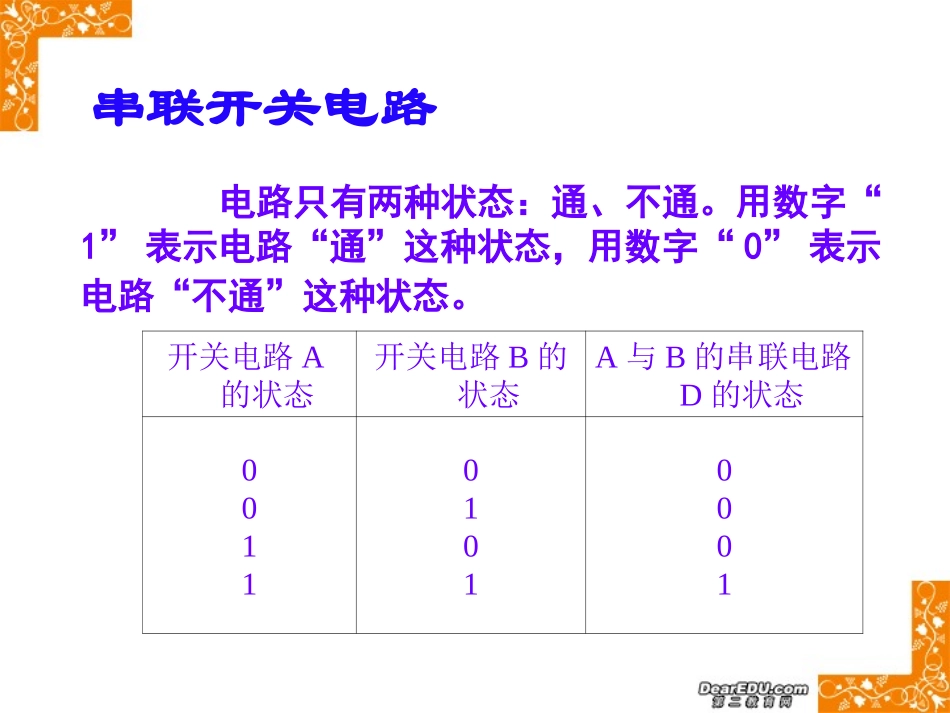
目录第一章开关电路开关电路(2)开关电路的数学表示(3)第二章布尔代数1.布尔代数(2)2.布尔代数模型—集合运算模型(1)3.布尔代数模型—命题运算模型(1)4.运算的比较(1)第三章布尔函数布尔多项式及其化简(2)布尔函数(2)第四章应用—开关电路设计开关电路设计(一)(1)开关电路设计(二)(1)一、开关电路的数学表示串联开关电路并联开关电路逆反开关电路串联开关电路电路只有两种状态:通、不通。用数字“1”表示电路“通”这种状态,用数字“0”表示电路“不通”这种状态。开关电路A的状态开关电路B的状态A与B的串联电路D的状态001101010001并联开关电路电路只有两种状态:通、不通。用数字“1”表示电路“通”这种状态,用数字“0”表示电路“不通”这种状态。开关电路A的状态开关电路B的状态A与B的并联电路D的状态001101010111逆反开关电路电路只有两种状态:通、不通。用数字“1”表示电路“通”这种状态,用数字“0”表示电路“不通”这种状态。开关电路A的状态A的逆反电路的状态0110A二、开关电路的数学模型——0-1布尔代数集合{0,1}与三种运算+,·,′其运算规律:加法:0+0=0,0+1=1+0=1,1+1=1;乘法:0·0=0,0·1=0,1·0=0,1·1=1;逆:0‘=1,1‘=0。构成一个重要的数学模型。我们称其为0-1布尔代数,记为{{0,1};+,·,′}。0-1布尔代数三、布尔代数与实数运算的异同{0,1}上的布尔加法、乘法运算与实数R上的加法、乘法运算有相同的性质,这些相同的性质主要有:(1){0,1}上的布尔加法运算与实数R上的加法运算都满足结合律、交换律;(2){0,1}上的布尔乘法运算与实数R上的乘法运算都满足结合律、交换律;(3){0,1}上的布尔加法、乘法运算与实数R上的加法、乘法运算都满足乘法对加法的分配律。(4)它们的加法运算都有0元。相同点不同点在布尔代数中一个最基本的性质是:1+x=1,称之为0-1律,这是与实数运算最不同的性质。由这一条性质和布尔代数的其他性质,可以验证以下性质:加法对乘法的分配律:x+yz=(x+y)(x+z)吸收律:x+xy=x,x(x+y)=x幂等律:x+x=x,x·x=x但实数R上的加法、乘法运算不满足加法对乘法的分配律、吸收律、幂等律。实数R上的运算的有些性质{0,1}上的布尔运算不满足。如,对于任意aR∈,有-aR∈,使得a+(-a)=0,即R中每一个数都有它的相反数。由于0-1律,所以{0,1}上的布尔加法运算不满足上面的性质。不同点在布尔代数中,有一种特殊的运算——求逆。在实数中不具有这种运算。布尔代数具有以下性质:(x+y)’=x’y’;(xy)’=x’+y’.通常称之为德莫根公式。这些不同点在电路设计、布尔多项式、布尔函数中发挥作用。例如,一元布尔多项式没有高次项。四、一般的布尔代数任给一个集合M,它的元素可以是有限个,也可以是无限多个,若对集合的元素定义了一个加法运算“+”,一个乘法运算“·”和一个逆运算“′”,且这三种运算都具有封闭性(即运算的结果还是M中的元素),若这些运算满足结合律、交换律、分配律、吸收律、互补律、0-1律、德莫根律、幂等律、双重逆反律九条性质,就称{M;+,·,′}是一个布尔代数。布尔代数五、布尔代数的两个具体例子集合运算命题运算集合P(X)与P(X)上的三种运算∪、∩、CX构成一个布尔代数的模型,记为{P(X);∪、∩、CX}。集合运算集合运算我们可以推出P(X)上的三种运算“∪”、“∩”、“CX”满足如下性质:(1)结合律(AB∪)∪C=A∪(B∪C)(A∩B)∩C=A∩(B∩C)(2)交换律AB=BA∪∪,A∩B=B∩A(3)分配律A∩(BC∪)=(A∩B)∪(A∩C)(交对并的分配律)A∪(B∩C)=(AB∪)∩(AC∪)(并对交的分配律)集合运算(4)吸收律A∪(A∩B)=A,A∩(AB∪)(5)互补律ACXA=X∪,A∩CXA=(6)—X律AX=X∪,A∩=(7)德莫根律CX(AB∪)=CXA∩CXB;CX(A∩B)=CXACXB∪(8)幂等律AA=A∪,A∩A=A(9)双重求补律CX(CXA)=A把所有命题的集合记为M。这样,“,,”就构成集合M上的三种运算。由于集合M上的三种运算“,,”满足布尔代数模型的九条性质,所以,集合M与三种运算“,,”构成一个...