高中数学 二项式系数的性质课件 北师大版选修2-3 课件VIP免费

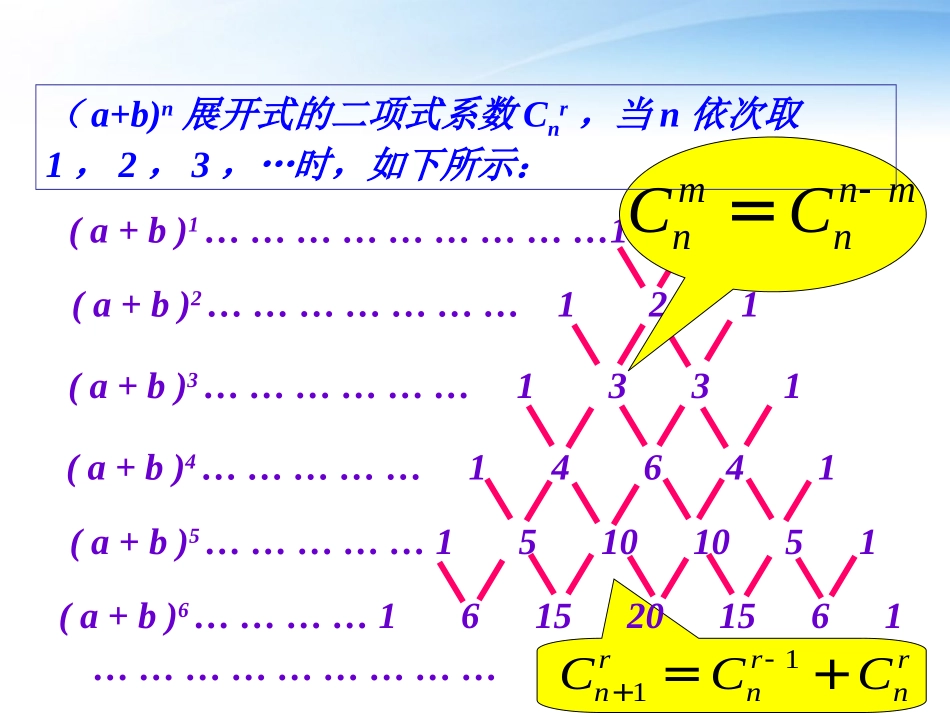
1、二项式定理：2、通项公式：011()nnnrnrrnnnnnnabCaCabCabCb--+=+++++1,(0,1,2,)rnrrrnTCabrn-+==3、说出(a+b)10的展开式中各项的二项式系数：0123456789101010101010101010101010,,,,,,,,,,CCCCCCCCCCC其中叫作二项式系数rnC(a+b)1………………………11(a+b)2…………………121(a+b)3………………1331(a+b)4……………14641(a+b)5……………15101051(a+b)6…………1615201561………………………（a+b)n展开式的二项式系数Cnr，当n依次取1，2，3，…时，如下所示：11rrrnnnCCC-+=+mnmnnCC-=这样的二项式系数表，早在我国南宋数学家杨辉1261年所著的《详解九章算法》一书里就已经出现了，在这本书里，记载着类似下面的表：一一一一二一一三三一一四六四一一五十十五一一六十五二十十五六一这个表称为杨辉三角在欧洲，这个表被认为是法国数学家帕斯卡(1623年—1662年）首先发现的杨辉三角的发现要比欧洲早五百年左右，由此可见我国古代数学的成就是非常值得中华民族自豪的．11121133114641151010511615201561与首末两端“等距离”的两个二项式系数相等性质1：对称性mnnmnCC性质2：增减性与最大值当n是偶数时，中间的一项二项式系数取得最大值；2nnC先增后减当n是奇数时，中间的两项二项式系数和相等，且同时取得最大值．12nnC12nnC性质3：各二项式系数的和15314202nnnnnnnCCCCCC1.(1x)﹣13的展开式中系数最小的项是（）(A)第六项(B)第七项（C）第八项(D)第九项C2.0.1.1.()()(,)32(.22312420443322104）的值为则若DCBAaaaaaxaxaxaxaax3、已知的展开式中只有第10项系数最大，求第五项。nxx431解：依题意，n为偶数，且,18,1012nnA453060xT项是展开式中的含、xxx5)11(5nnnnnnnCCCC31279311321)(、化简2、化简(2x+1)5-5(2x+1)4+10(2x+1)3-10(2x+1)2+5(2x+1)-1=.则若||||||||,)21(.482108822108aaaaxaxaxaax3、求(a+b+c)10的展开式经合并同类项后的项数45x8366532xn)2(（1）求(x+2y)7展开式中系数最大的项（2）求(x-2y)7展开式中系数最大的项（2）展开式中共有8项，系数最大必为正项，即在第一、三、五、七这四项中取得，又因(x-2y)7括号内两项中后项系数绝对值大于前项系数的绝对值，故系数最大必在中间或偏右，故只需要比较T5和T7两项系数大小即可．66744775)2()2(CCTT系数系数141737CC所以系数最大的项是第五项4334475560)2(yxxyCT性质1：对称性性质2：增减性与最大值性质3：各二项式系数的和与首末两端“等距离”的两个二项式系数相等当n是偶数时，中间的一项二项式系数取得最大值；2nnC先增后减当n是奇数时，中间的两项二项式系数和相等，且同时取得最大值．12nnC12nnC15314202nnnnnnnCCCCCC