高中数学 双曲线的简单几何性质一课件 北师大版选修2-1 课件VIP免费

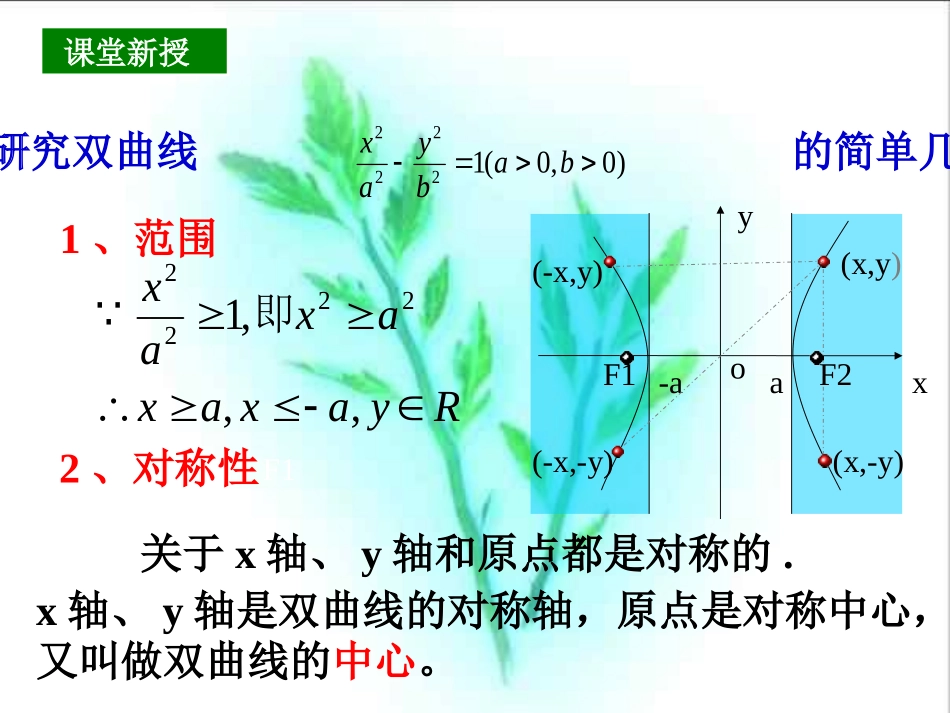
§3.2双曲线的性质222bac定义定义图象图象标准方程标准方程焦点坐标焦点坐标a.b.ca.b.c的关系的关系||MF1|-|MF2||=2a（０<2a<|F1F2|）F(±c,0)F(0,±c))0,0(12222babyax)0,0(12222babxayyxoF2F1MxyF2F1M复习回顾:2、对称性一、研究双曲线的简单几何性质)0,0(12222babyax1、范围Ryaxaxaxax,,,12222即关于x轴、y轴和原点都是对称的.x轴、y轴是双曲线的对称轴，原点是对称中心，又叫做双曲线的中心。xyo-aa(-x,-y)(-x,y)(x,y)(x,-y)课堂新授课堂新授F1F2F13、顶点（1）双曲线与对称轴的交点，叫做双曲线的顶点xyo-b1B2Bb1A2A-aa)0,()0,(21aAaA、顶点是如图，线段叫做双曲线的实轴，它的长为2a,a叫做实半轴长；线段叫做双曲线的虚轴，它的长为2b,b叫做双曲线的虚半轴长2A1A2B1B（2）实轴与虚轴等长的双曲线叫等轴双曲线（3）)0(22mmyxm>0表示焦点在x轴上的双曲线；m<0表示焦点在y轴上的双曲线。M(x,y)4、渐近线1A2A1B2BN(x,y’):的位置关系它与xaby:的位置的变化趋势它与xaby的下方在xaby慢慢靠近xyoxabyxabyabxabybabyax的渐近线为双曲线)0,0(12222（1）的渐近线为等轴双曲线)0(22mmyx（2）xy5、离心率双曲线的叫做的比双曲线的焦距与实轴长,ace离心率。c>a>0e>1（1）定义：（2）e的范围：（3）e的含义：11)(2222eacaacab,,的开口就越大双曲线越大决定双曲线的开口大小abab（4）等轴双曲线的离心率e=?2的双曲线是等轴双曲线离心率2ee是表示双曲线开口大小的一个量,e越大开口越大也越大越大，eab?)0,0(12222的简单几何性质你能导出双曲线babxay)0,0(12222babxay)0,0(12222babyax标准方程图形范围对称性顶点焦点离心率渐近线xyoF1F2xyoRyax,对称轴：x轴,y轴中心：原点)0,(ae>1,Rxay,对称轴：x轴,y轴中心：原点),0(ae>1,e越大，张口开阔e越小，张口扁狭e越大，张口开阔e越小，张口扁狭xabyxbay(c,0)(-c,0)(0,c)(0,-c)F1F2例1:求双曲线的实半轴长、虚轴长、焦点坐标、顶点坐标、离心率、渐近线方程。解:由题意可得实半轴长:虚轴长:焦点坐标:离心率:渐近线方程:32yxa=222143xy223b(7,0),(7,0)72cea顶点坐标:(-2,0)，(2,0)21?3y2x问:若双曲线的方程为呢43a24b(0,7),(0,7)213cea32yx(0,3),(0,3)例题讲解例题讲解共轭双曲线问:若将题目中“焦点在y轴上”改为“焦点在坐标轴上”呢?先定型，再定量例2.4516线和焦点坐标程，并且求出它的渐近出双曲线的方轴上，中心在原点，写焦点在，，离心率离是已知双曲线顶点间的距xe本节课的学习,你有哪些收获?(1)由双曲线的图象得其几何性质;(2)求双曲线标准方程应先定型,再定量.