高中数学 3.3.1函数的单调性与导数课件 新人教A版选修1 1 课件VIP免费

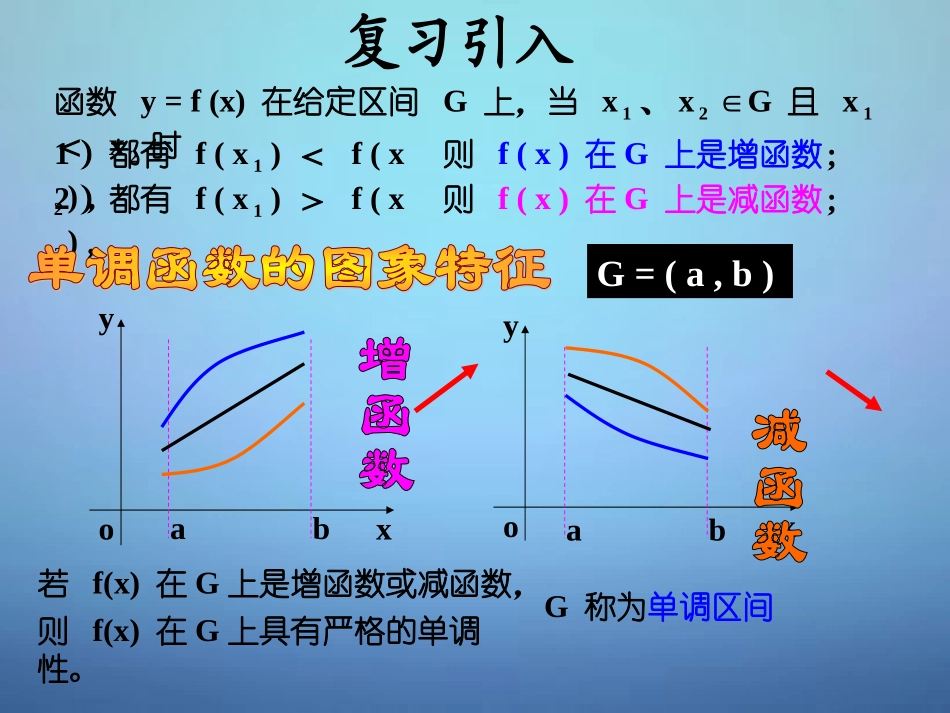
3.3.1函数的单调性与最值3.3.1函数的单调性与最值高二数学选修1-1课题：函数的单调性与导数教学目标•1.正确理解并利用导数判断函数的单调性的原理•2.掌握利用导数判断函数单调性的方法•3.会利用导数求函数的单调区间•4.利用图像为结论通过观察分析、归纳总结等方式，培养学生的数形结合思想重点难点教学重点：利用导数判断函数单调性并求出单调区间教学难点：利用导数的几何意义探究函数的单调性函数y=f(x)在给定区间G上，当x1、x2G∈且x1＜x2时yxoabyxoab1）都有f(x1)＜f(x2)，则f(x)在G上是增函数；2）都有f(x1)＞f(x2)，则f(x)在G上是减函数；若f(x)在G上是增函数或减函数，则f(x)在G上具有严格的单调性。G称为单调区间复习引入G=(a,b)观察:下图(1)表示高台跳水运动员的高度h随时间t变化的函数的图象,图(2)表示高台跳水运动员的速度v随时间t变化的函数的图象.运动员从起跳到最高点,以及从最高点到入水这两段时间的运动状态有什么区别?2()4.96.510httt()9.86.5vtt①运动员从起跳到最高点,离水面的高度h随时间t的增加而增加,即h(t)是增函数.相应地,.0)()(thtv②从最高点到入水,运动员离水面的高度h随时间t的增加而减少,即h(t)是减函数.相应地,()()0.vthtOabth(1)abtvO(2)xyOxyOxyOxyOy=xy=x2y=x3xy1观察下面一些函数的图象,探讨函数的单调性与其导函数正负的关系.结论在某个区间(a,b)内,如果,那么函数在这个区间内单调递增;如果,那么函数在这个区间内单调递减.0)(xf)(xfy0)(xf)(xfy如果恒有，则是常数。)(xf()0fx例1已知导函数的下列信息:()fx当14,或x<1时,当x=4,或x=1时,()0;fx()0;fx()0.fx试画出函数的图象的大致形状.()fx解:当14,或x<1时,可知在此区间内单调递减;()0,fx()fx当x=4,或x=1时,()0.fx综上,函数图象的大致形状如右图所示.()fxxyO14例2判断下列函数的单调性,并求出单调区间:32(1)()3;(2)()23;fxxxfxxx(3)()sin,(0,);fxxxx32(4)()23241.fxxxx解:(1)因为,所以xxxf3)(322()333(1)0.fxxx因此,函数在上单调递增.3()3fxxxxR单调递增区间为(-,+)(2)因为,所以32)(2xxxf()222(1).fxxx当,即时,函数单调递增;()0fx1x2()23fxxx当,即时,函数单调递减.()0fx1x2()23fxxx单调递增区间为(1,+);单调递减区间为(-,1);例2判断下列函数的单调性,并求出单调区间:32(1)()3;(2)()23;fxxxfxxx(3)()sin,(0,);fxxxx32(4)()23241.fxxxx解:(3)因为,所以),0(,sin)(xxxxf()cos10.fxx因此,函数在上单调递减.()sinfxxx(0,)x例2判断下列函数的单调性,并求出单调区间:32(1)()3;(2)()23;fxxxfxxx(3)()sin,(0,);fxxxx32(4)()23241.fxxxx(4)因为,所以当,即时,函数单调递增;()0fx11711722xx或()fx当,即时,函数单调递减.()0fx2()6624fxxx11711722x()fx单调递增区间为(-1+172,+);(-,-1-172);单调递减区间为(-1-172,-1+172)例2判断下列函数的单调性,并求出单调区间:32(1)()3;(2)()23;fxxxfxxx(3)()sin,(0,);fxxxx32(4)()23241.fxxxx（1）求函数的定义域（2）求函数的导数（3）令f’(x)>0以及f’(x)<0,求自变量x的取值范围（4）下结论，写出函数的单调区间。总结:用“导数法”求单调区间的步骤：;)()2(;42)()1(2xexfxxxfx.)()4(;3)()3(233xxxxfxxxf1.判断下列函数的单调性,并求出单调区间:ab(,)在某个区间内,fx'()0fxab()(,)在内单调递增fx'()0()(,)fxab在内单调递减注意：应正确理解“某个区间”的含义,它必是定义域内的某个区间。证明:因为f(x)=2x3-6x2+7f/(x)=6x2-12x=6x(x-2),当x∈(0,2)时,f/(x)=6x(x-2)<0,函数f(x)=2x3-6x2+7在(0,2)内是减函数例求证函数f(x)=2x3-6x2+7在(0,2)内是减函数证明可导函数f(x)在(a,b)内的单调性的方法：(1)求f’(x)；(2)确认f’(x)在(a,b)内...