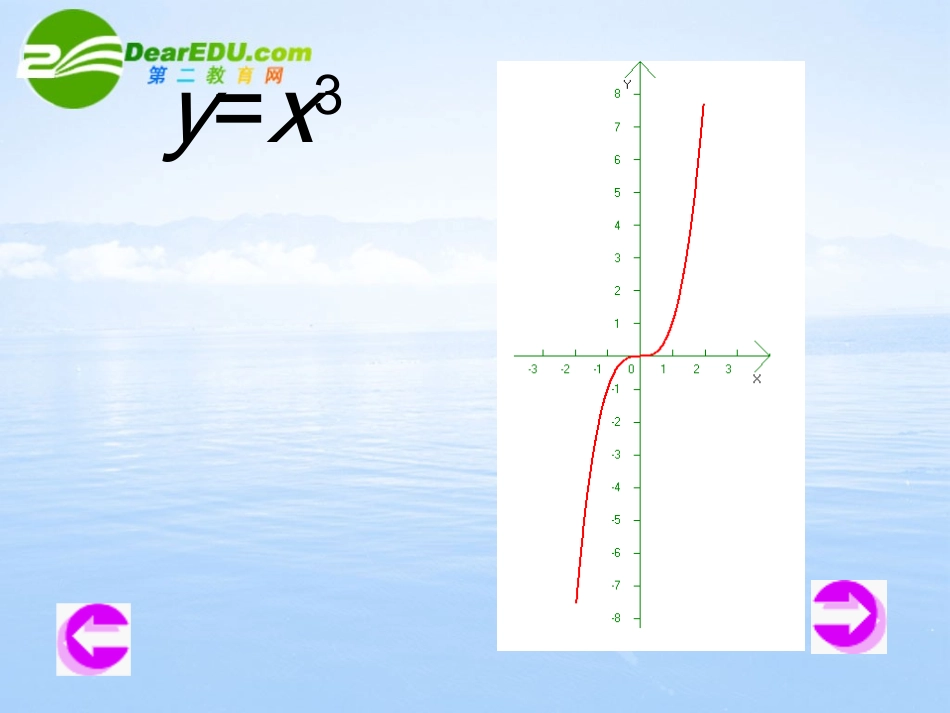
25/2/26函数的单调性25/2/26y=x2从图象可以看到:图象在y轴的右侧部分是上升的,也就是说,当x在区间[0,+)上取值时,随着x的增大,相应的y值也增大,即如果取x1,x2[0,+),得到y1=f(x1),y2=f(x2),那么当x1y2。这时我们就说函数y=x2在(-,0)上是减函数。x1x2y1y2x2x1y2y125/2/26y=x325/2/26如果对于属于定义域I内某个区间上的任意两个自变量的值x1,x2,当x1f(x2),那么就说f(x)在这个区间上是减函数y=f(x)f(x1)f(x2)x1x225/2/26如果函数y=f(x)在某个区间是增函数或是减函数,那么就说函数y=f(x)在这一区间具有(严格的)单调性,这一区间中做y=f(x)的单调区间。在单调区间上增函数的图象是上升的,减函数的图象是下降的。25/2/26例1:下图是定义在闭区间[-5,5]上的函数y=f(x)的图象,根据图象说出y=f(x)的单调区间,以及在每一个单调区间上,y=f(x)是增函数还是减函数。解:函数y=f(x)的单调区间有[-5,-2),[-2,1),[1,3),[3,5],其中y=f(x)在区间[-5,-2),[1,3)上是减函数,在区间[-2,1),[3,5]上是增函数。y=f(x)25/2/26例2:证明函数f(x)=3x+2在R上是增函数。证明:设x1,x2是R上的任意两个实数,且x1