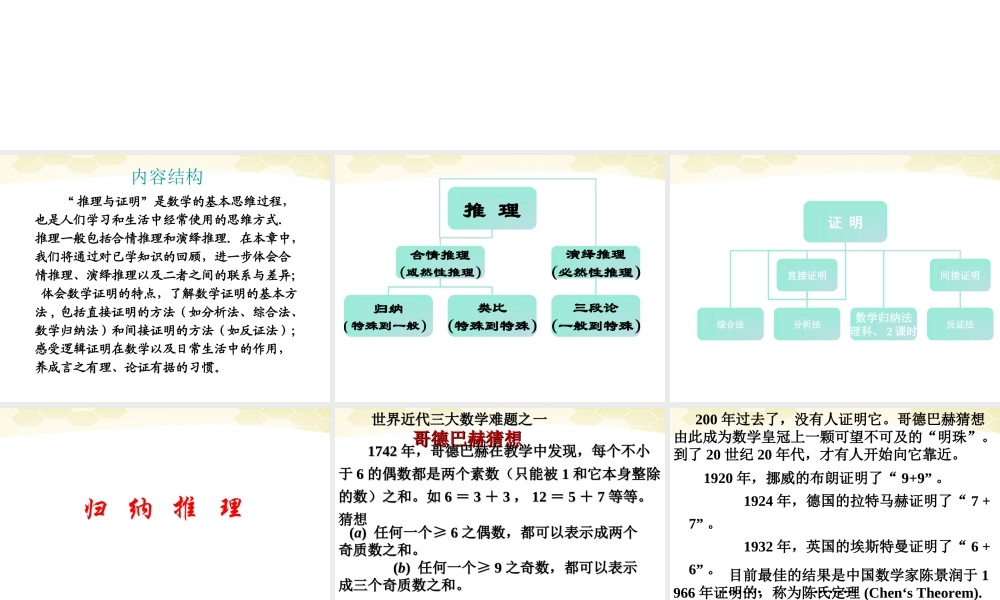
内容结构 “ 推理与证明”是数学的基本思维过程,也是人们学习和生活中经常使用的思维方式.推理一般包括合情推理和演绎推理.在本章中,我们将通过对已学知识的回顾,进一步体会合情推理、演绎推理以及二者之间的联系与差异; 体会数学证明的特点,了解数学证明的基本方法 , 包括直接证明的方法(如分析法、综合法、数学归纳法)和间接证明的方法(如反证法);感受逻辑证明在数学以及日常生活中的作用,养成言之有理、论证有据的习惯。 推 理合情推理(或然性推理)演绎推理(必然性推理)归纳( 特殊到一般)类比(特殊到特殊)三段论(一般到特殊) 证 明直接证明间接证明综合法分析法反证法数学归纳法(理科、 2 课时) 归 纳 推 理 哥德巴赫猜想哥德巴赫猜想 世界近代三大数学难题之一 世界近代三大数学难题之一 17421742 年,哥德巴赫在教学中发现,每个不小年,哥德巴赫在教学中发现,每个不小于于 66 的偶数都是两个素数(只能被的偶数都是两个素数(只能被 11 和它本身整除和它本身整除的数)之和。如的数)之和。如 66 == 33 ++ 33 ,, 1212 == 55 ++ 77 等等。等等。猜想 ((aa) ) 任何一个≥任何一个≥ 66 之偶数,都可以表示成两个之偶数,都可以表示成两个奇质数之和。奇质数之和。 ((bb) ) 任何一个≥任何一个≥ 99 之奇数,都可以表示之奇数,都可以表示成三个奇质数之和。 成三个奇质数之和。 有人对 33×108 以内且大过 6 之偶数一一进行验算,哥德巴赫猜想 (a) 都成立。 目前最佳的结果是中国数学家陈景润于 1966 年证明的,称为陈氏定理 (Chen‘s Theorem).“ 任何充份大的偶数都是一个质数与一个自然数之和,而后者仅仅是两个质数的乘积” , 通常都简称这个结果为大偶数可表示为 “ 1+2” 的形式。 1920 年,挪威的布朗证明了“ 9+9” 。 1924 年,德国的拉特马赫证明了“ 7 + 7” 。 1932 年,英国的埃斯特曼证明了“ 6 + 6” 。 ……… ……… 200 年过去了,没有人证明它。哥德巴赫猜想由此成为数学皇冠上一颗可望不可及的“明珠”。到了 20 世纪 20 年代,才有人开始向它靠近。 1637 年,法国数学家费马提出: “将一个立方数分为两个立方数的和,一个四次幂分为两个四次幂的和,或者一般地将一个高于二次的幂分为两个同次的幂的和,这是不可能的 .”费马猜想费马猜想数论中最著名的世界难题之一数论中最著名的...