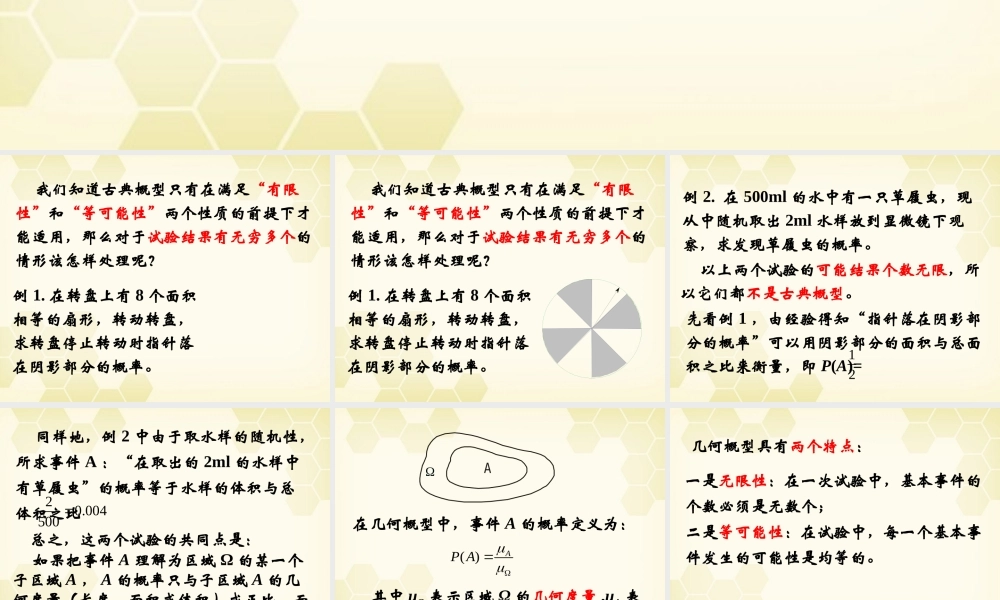
3.3.1 几何概型 我们知道古典概型只有在满足“有限性”和“等可能性”两个性质的前提下才能适用,那么对于试验结果有无穷多个的情形该怎样处理呢? 例 1. 在转盘上有 8 个面积相等的扇形,转动转盘,求转盘停止转动时指针落在阴影部分的概率。 我们知道古典概型只有在满足“有限性”和“等可能性”两个性质的前提下才能适用,那么对于试验结果有无穷多个的情形该怎样处理呢? 例 1. 在转盘上有 8 个面积相等的扇形,转动转盘,求转盘停止转动时指针落在阴影部分的概率。 例 2. 在 500ml 的水中有一只草履虫,现从中随机取出 2ml 水样放到显微镜下观察,求发现草履虫的概率。 以上两个试验的可能结果个数无限,所以它们都不是古典概型。先看例 1 ,由经验得知“指针落在阴影部分的概率”可以用阴影部分的面积与总面积之比来衡量,即 P(A)=12 同样地,例 2 中由于取水样的随机性,所求事件 A :“在取出的 2ml 的水样中有草履虫”的概率等于水样的体积与总体积之比20.004500 总之,这两个试验的共同点是: 如果把事件 A 理解为区域 Ω 的某一个子区域 A , A 的概率只与子区域 A 的几何度量(长度、面积或体积)成正比,而与 A 的位置和形状无关,则称满足以上条件的试验为几何概型 . AΩ在几何概型中,事件 A 的概率定义为:( )AP A 其中 μΩ 表示区域 Ω 的几何度量 ,μA 表示子区域 A 的几何度量 . 几何概型具有两个特点:一是无限性:在一次试验中,基本事件的个数必须是无数个;二是等可能性:在试验中,每一个基本事件发生的可能性是均等的。 例 3. 随机事件 A :“从正整数中任取两个数,其和为偶数”是否为几何概型。 解:尽管这里事件满足几何概型的两个特点:有无限多个基本事件,且每个基本事件的出现是等可能的,但它不满足几何概型的基本特征——能进行几何度量。所以事件 A 不是几何概型。 例 4. 下列随机试验是否为几何概型?为什么? ( 1 )经过严格训练的枪手的打靶;( 2 )某学生从家里到达学校所用的时间。答案:( 1 )不是;( 2 )是。 例 5. 一海豚在水池中自由游弋,水池为长 30 m ,宽 20 m 的长方形,求此刻海豚嘴尖离岸边不超过 2 m 的概率 . 30 m20 m2 m解:对于几何概型,关键是要构造出随机事件对应的几何图形,利用图形的几何度量来求随机事件的概率 . 如图,区域 Ω 是长30 m 、宽 20 ...