7.2正切函数的图像与性质-(2)VIP免费

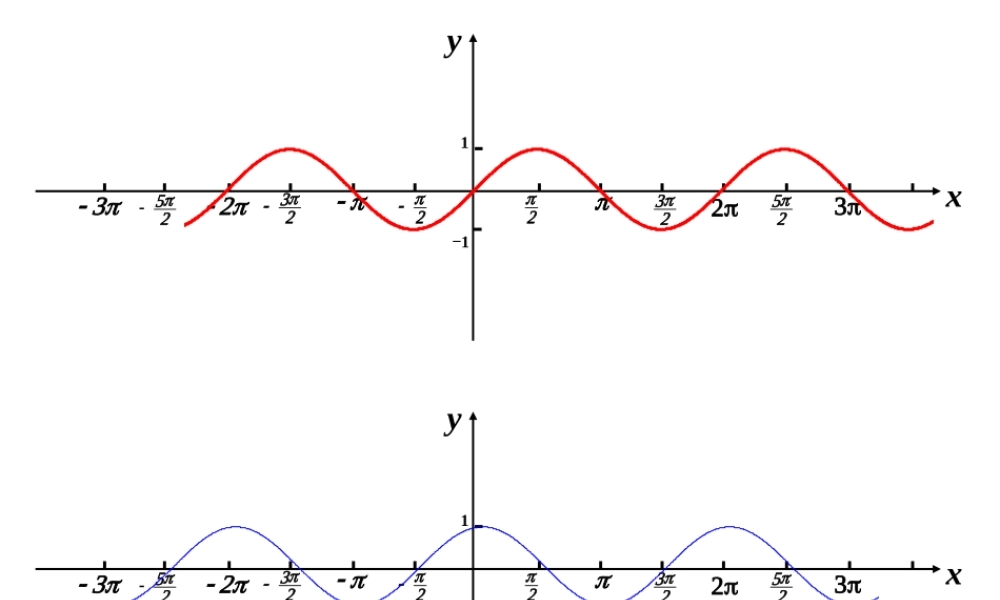
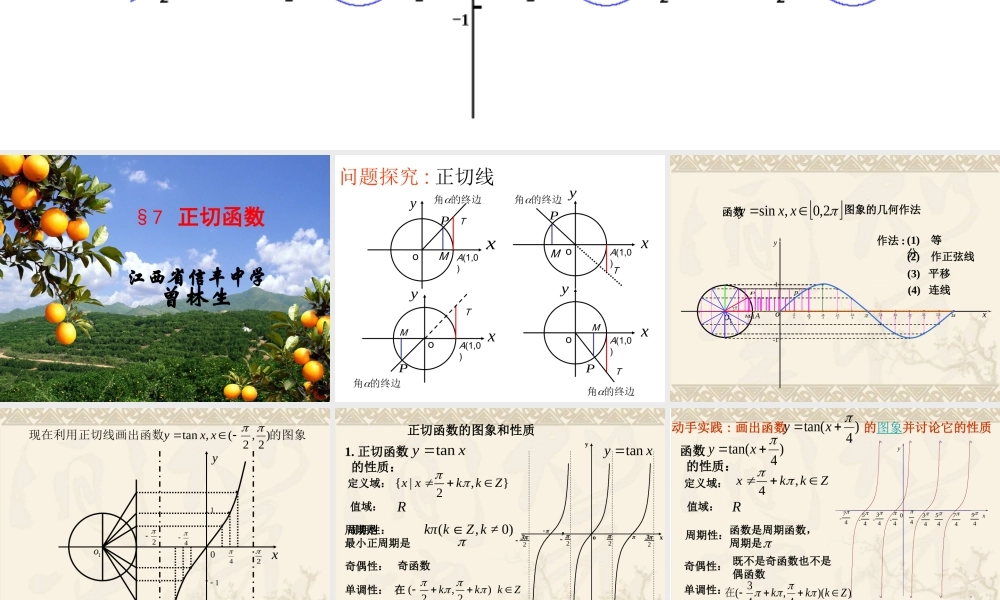
xy1-1    xy1-1    §7 正切函数曾林生江西省信丰中学问题探究 : 正切线的终边角MA(1,0)o的终边角yxPTA(1,0)oyxPA(1,0)o的终边角MyPxTTMA(1,0)oTM的终边角yxP2 函数2,0,sinxxy图象的几何作法oxy---11---1--1oA作法 : (1) 等分3232656734233561126(2) 作正弦线(3) 平移61P1M/1p(4) 连线的图象数现在利用正切线画出函)2,2(,tanxxy2xy4421101otan ,(,)2 2yx x  演示正切函数的图象和性质1. 正切函数 的性质：tanyx定义域： { |,}2x xkkZ值域：R周期性：奇偶性： 奇函数单调性： 在 (,)22 kkkZ上是增加的 .xy 22 o22 tan yx周期是 ,最小正周期是 )0≠,∈(kZkπk对称性：)∈)(0+2()0,(Zk，πkππk和对称中心是 ，无对称轴 .动手实践 : 画出函数 的图象并讨论它的性质函数 的性质：定义域：值域：R周期性：函数是周期函数，周期是 奇偶性： 既不是奇函数也不是偶函数单调性：)4tan(xy)4tan(xyZkkx,4是增加的在))(4,43(Zkkk对称性：)∈)(0+4()0,+4Zk，πkππkπ和对称中心是 ( 一 ，无对称轴 .- 74- 54494- 3474-454340yx图象正切函数值域性 质周期性单调性奇偶性对称性定义域类 比数形结合让我们一起回顾我们的快乐学习旅程 !画出函数 的图象并讨论它的性质 .)2tan(xy1 、课外探究 :2 、作业习题 1-7: 必做 A 组 1 、 3 选做 B 组 2xy 22 o22 44