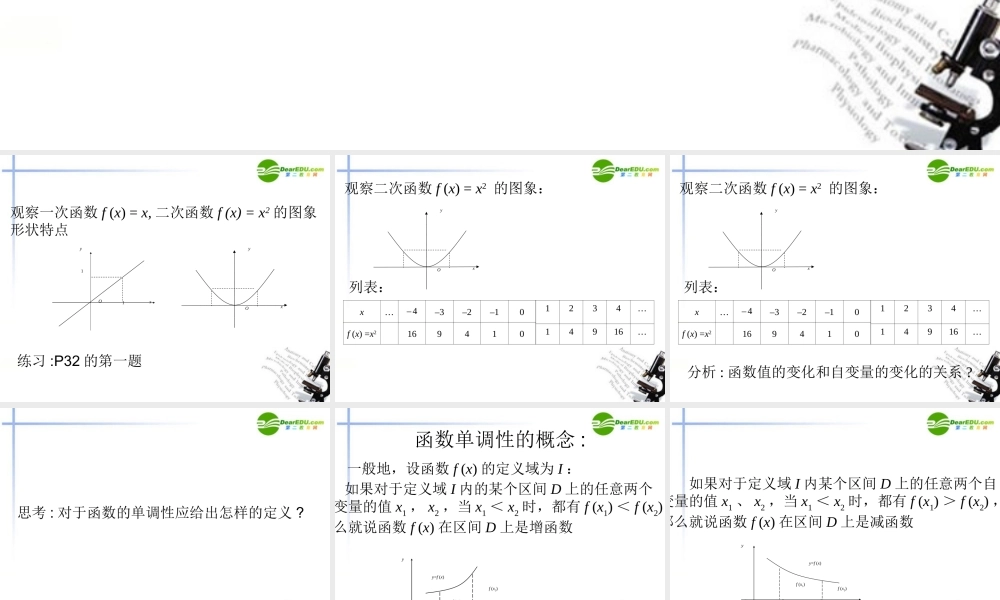
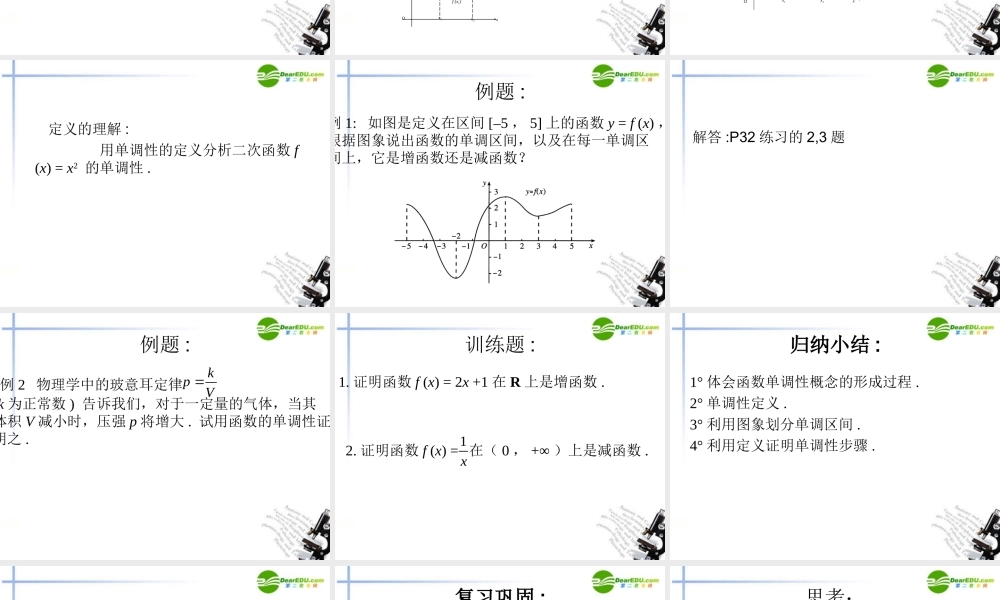
1.3.1 单调性与最大 ( 小 )值 观察一次函数 f (x) = x, 二次函数 f (x) = x2 的图象形状特点 yx11OOxy练习 :P32 的第一题 观察二次函数 f (x) = x2 的图象: Oxy列表:x…– 4–3–2–10f (x) =x21694101234…14916… 观察二次函数 f (x) = x2 的图象: Oxy列表:x…– 4–3–2–10f (x) =x21694101234…14916…分析 : 函数值的变化和自变量的变化的关系 ? 思考 : 对于函数的单调性应给出怎样的定义 ? 函数单调性的概念 :一般地,设函数 f (x) 的定义域为 I : 如果对于定义域 I 内的某个区间 D 上的任意两个自变量的值 x1 , x2 ,当 x1 < x2 时,都有 f (x1) < f (x2) ,那么就说函数 f (x) 在区间 D 上是增函数 xx1x2Oyf (x1)f (x2)y=f (x) 如果对于定义域 I 内某个区间 D 上的任意两个自变量的值 x1 、 x2 ,当 x1 < x2 时,都有 f (x1) > f (x2) ,那么就说函数 f (x) 在区间 D 上是减函数 xx1x2Oyf (x1)f (x2)y=f (x) 定义的理解 : 用单调性的定义分析二次函数 f (x) = x2 的单调性 . 例题 :例 1: 如图是定义在区间 [–5 , 5] 上的函数 y = f (x) ,根据图象说出函数的单调区间,以及在每一单调区间上,它是增函数还是减函数? 解答 :P32 练习的 2,3 题 例题 :例 2 物理学中的玻意耳定律kpV(k 为正常数 ) 告诉我们,对于一定量的气体,当其体积 V 减小时,压强 p 将增大 . 试用函数的单调性证明之 . 训练题 :1. 证明函数 f (x) = 2x +1 在 R 上是增函数 . 2. 证明函数 f (x) =1x在( 0 , +∞ )上是减函数 . 归纳小结 :1° 体会函数单调性概念的形成过程 .2° 单调性定义 .3° 利用图象划分单调区间 .4° 利用定义证明单调性步骤 . 第二课时 : 最大值和最小值 复习巩固 :• 1° 单调性定义• 2° 利用定义证明单调性步骤 思考:• 画出反比例函数 的图象 (1) 这个函数的定义域Ⅰ是什么 ? (2) 它在定义域Ⅰ上的单调性是怎样的 ? 证明你的 结论 .1( )f xx 作出下列三个函数的图象并观察21( ),( ),( )f xx f xxf xx 作出下列三个函数的图象并观察21( ),( ),( )f xx f xxf xxxy11OOxy观察图象是否存在最低点和最高点 ? 函数 f (x) = x2. 在 ( – ∞ , 0) 上是减函数, ...