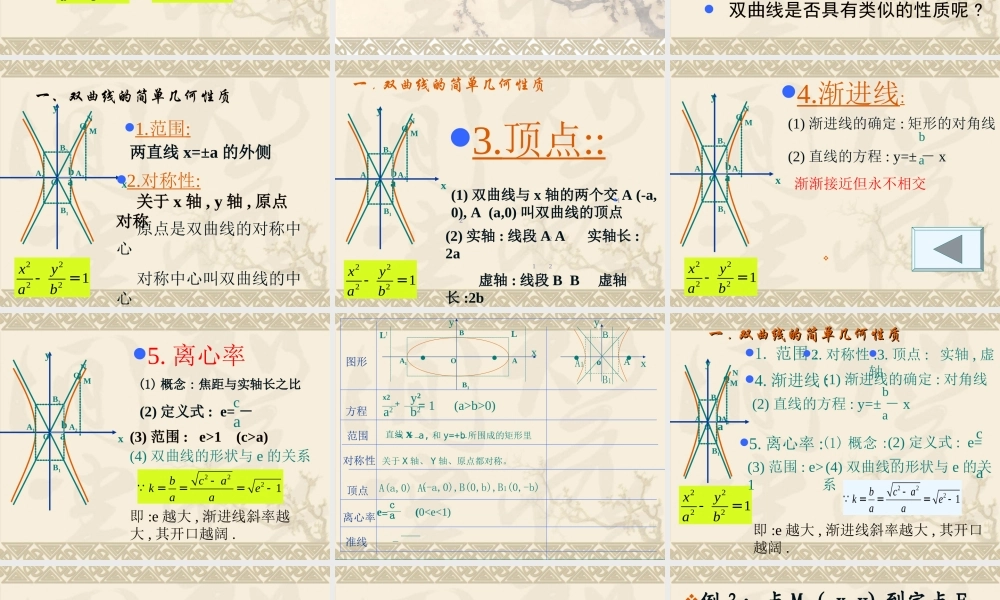
新课标人教版课件系列《高中数学》选修 1-1 2.2.2 《双曲线的简单几何性质》 教学目标 知识与技能目标 了解平面解析几何研究的主要问题:( 1 )根据条件,求出表示曲线的方程;( 2 )通过方程,研究曲线的性质.理解双曲线的范围、对称性及对称轴,对称中心、离心率、顶点、渐近线的概念;掌握双曲线的标准方程、会用双曲线的定义解决实际问题;通过例题和探究了解双曲线的第二定义,准线及焦半径的概念,利用信息技术进一步见识圆锥曲线的统一定义.. 过程与方法目标 ( 1 )复习与引入过程 引导学生复习得到椭圆的简单的几何性质的方法,在本节课中不仅要注意通过对双曲线的标准方程的讨论,研究双曲线的几何性质的理解和应用,而且还注意对这种研究方法的进一步地培养.①由双曲线的标准方程和非负实数的概念能得到双曲线的范围;②由方程的性质得到双曲线的对称性;③由圆锥曲线顶点的统一定义,容易得出双曲线的顶点的坐标及实轴、虚轴的概念;④应用信息技术的《几何画板》探究双曲线的渐近线问题;⑤探究双曲线的扁平程度量椭圆的离心率 56P 一 . 复习引入 1.双曲线的定义是怎样的? 2. 双曲线的标准方程是怎样的?22221xyab-=22221yxab-= 思考回顾 椭圆的简单几何性质 ? ① 范围 ; ② 对称性 ; ③ 顶点 ; ④ 离心率等 双曲线是否具有类似的性质呢 ? 回想:我们是怎样研究上述性质的? 一、双曲线的简单几何性质 yB2A1A2 B1 xOb aM NQ1.范围:两直线 x=±a 的外侧2.对称性: 关于 x 轴 , y 轴 , 原点对称 原点是双曲线的对称中心 对称中心叫双曲线的中心22221xyab-= 一 . 双曲线的简单几何性质yB2A1A2 B1 xOb aM NQ3.顶点::(1) 双曲线与 x 轴的两个交 A (-a,0), A (a,0) 叫双曲线的顶点22221xyab-=12(2) 实轴 : 线段 A A 实轴长 :2a 虚轴 : 线段 B B 虚轴长 :2b 1 2 1 2 yB2A1A2 B1 xOb aM NQ22221xyab-=4.渐进线: (1) 渐进线的确定 : 矩形的对角线 (2) 直线的方程 : y=± - xba渐渐接近但永不相交 (1) 概念 : 焦距与实轴长之比yB2A1A2 B1 xOb aM NQ5. 离心率(2) 定义式 : e= - c a(3) 范围 : e>1 (c>a)(4) 双曲线的形状与 e 的关系2221bcakeaa-===-即 :e 越大 , 渐进线斜率越大 , 其开口越阔 . 关于 X 轴、 Y 轴、原点都对称。 图形方程范围...