高中数学(微积分基本定理)课件2 新人教A版选修2-2 课件VIP免费

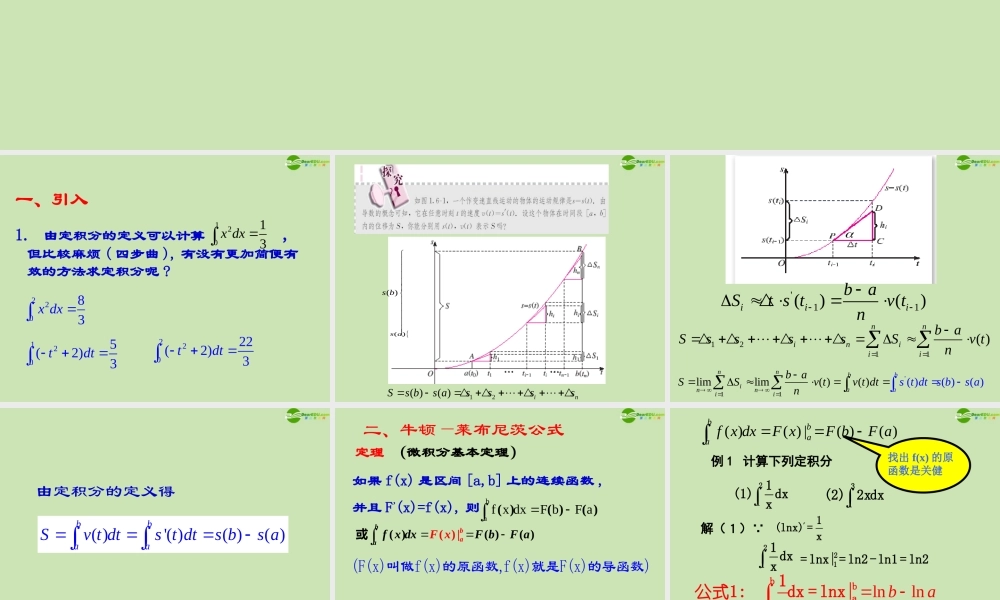
1.6 微积分基本定理1. 由定积分的定义可以计算 , 但比较麻烦 ( 四步曲 ), 有没有更加简便有效的方法求定积分呢 ?12013x dx 一、引入1205(2)3tdt22022(2)3tdt22083x dx 12( )( )inSs bs assss  ( )s b ( )s a'11()()iiibaSt s tv tn 1211( )nniniiibaSssssSv tn  1'1limlim( )(( ))( )( )nnbibniaanibaSSv tv ts t dt s bstnad  由定积分的定义得'( )( )( )( )baba s t dSv t dtts bs a定理 （微积分基本定理）二、牛顿—莱布尼茨公式( )|( )( )( )bbaaf x dxF bxFFa或(F(x)叫做f(x)的原函数,f(x)就是F(x)的导函数) 如果 f(x) 是区间 [a,b] 上的连续函数 ,并且 F’(x)=f(x), 则ba f x dxF bF a ( )( )( )例 1 计算下列定积分 211(1)dxx解（１）∵1(lnx) = xlnlnbabbaa1公式1: dx = lnx|x31(2) 2xdx3221|318321(2) 2xdx = x21= lnx| = ln2 -ln1 = ln2211 dxx( )( ) |( )( )bbaa f x dxF xF bF a找出 f(x) 的原函数是关健 练习： 101013023-1(1) 1dx = ______(2) xdx = ______(3) x dx = ______(4)x dx = ______nxn+1bbaax公式2: dx =|n +111/21/415/4复习 : 定积分的基本性质 性质 1. dx)]x(g)x(f[bababadx)x(gdx)x(f性质 2. badx)x(kf badx)x(fk例 ２．计算下列定积分 原式33221111()dxdxdxdxxx332211=3x3x解 :∵32211(3x -)dxx211)xx32(x ) = 3x , (3311176(31 )()313x3 3311= x ||( )( ) |( )( )bbaa f x dxF xF bF a 练习： ______(1)xe12022122-121(1) (-3t + 2)dt1(2) (x +) dx = ______x(3) (3x + 2x -1)dx = ______(4)dx = ______23/619e2-e+1( )( ) |( )( )bbaa f x dxF xF bF a例 ３．计算下列定积分 20(2)cosxdx0(1)sinxdx解（ 1 ）∵'(s )sinco xx00 sin(s ) |cos( cos0)1 12xdxco x    思考 :( )a的几何意义是什么0 sinxdx?22( )( )bc00sinxdx = _______sinxdx = _______0120(2)cosxdx2200 cossin|sinsin 01 012xdxx '(sin )cosxx解思考 :2( )a的几何意义是什么0 cosxdx?2( )( )bc00cosxdx = _______cosxdx = _______00微积分基本公式)()()(aFbFdxxfba三、小结bbaa1公式1: dx = lnx|x牛顿－莱布尼茨公式沟通了导数与定积分之间的关系．nxn+1bbaax公式2: dx =|n +1 作业： P ６２ A 1 (2)(3)(5)(6)