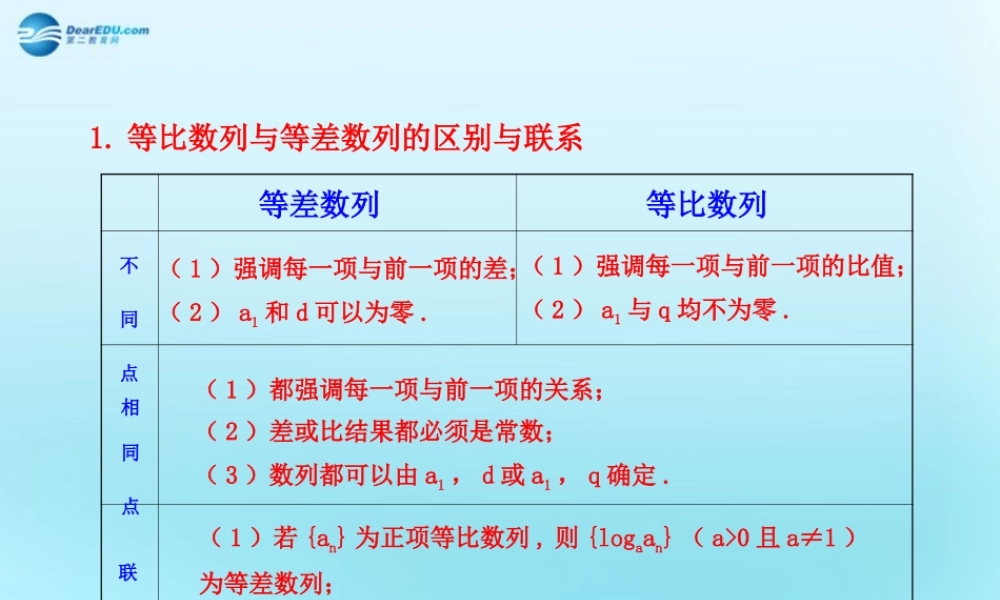
1. 等比数列与等差数列的区别与联系不同点等差数列( 1 )若 {an} 为正项等比数列 , 则 {logaan} ( a>0 且 a≠1 )为等差数列;( 2 )若 {an} 为等差数列,则 { } 为等比数列( b≠0 ) .( 1 )都强调每一项与前一项的关系;( 2 )差或比结果都必须是常数;( 3 )数列都可以由 a1 , d 或 a1 , q 确定 .等比数列相同点联系( 1 )强调每一项与前一项的比值;( 2 ) a1 与 q 均不为零 .( 1 )强调每一项与前一项的差;( 2 ) a1 和 d 可以为零 .nab2. 等比数列的前 n 项和等比数列前n项和公 比适用公式q=1q≠1n11Sna (a0)n1n1a 1 qS(a0,q0)1 q1nn1aa qS(a0,q0)1 q3. 等差、等比数列的判定方法定义法中项法an+1-an=d(d 为常数 )方法分类等差数列等比数列2an+1 = an+an+2 ( n∈N* )n 1naq(qaq0) 为常数,2n 1nn 2naaa(nN*a0),4. 等差、等比数列的性质条件等差数列m , n , p , q∈N*且 m+n=p+q项数成等差数列等比数列am+an=ap+aq am•an=ap•aq对应项仍成等差数列对应项仍成等比数列m∈N* , Sm 为前 n 项和 Sm≠0Sm,S2m-Sm,S3m-S2m,…仍成等差数列Sm,S2m-Sm,S3m-S2m,…仍成等比数列规定: 1. S 奇、 S 偶分别为数列中所有奇数项的和与所有偶数项的和2.TT奇偶、分别为数列中所有奇数项的积与所有偶数项的积条件等差数列项数为奇数时等比数列S 奇 -S 偶= a 中项数为偶数时TaT奇中偶=nSSd2偶奇=n2TqTSqS偶奇偶奇==等差数列 {an}等比数列 {an}定义⑴ 通项公式⑵ 推导方法性质前 n 项和 Sn⑴ 公式⑵ 推导方法an+1-an=d( 常数 )an+1 / an=q( 不为零的常数 )an=a1+(n–1)dan-am=(n–m)dan=a1 qn-1an / am=qn-m① 归纳猜想验证法② 首尾相咬累加法① 归纳猜想验证法② 首尾相咬累乘法若 m+n=r+s,m , n ,r , s∈N*则 am+an=ar+as若 m+n=r+s,m , n , r , s∈N*则 am·an=ar·as1nn1(aa )nS2n(n1)nad2当 q = 1 时Sn=na1当 q≠1 时n11nna (1 q )aa qS1 q1 q化零为整法① 归纳猜想验证法②错项相减法5. 等差数列与等比数列的比较