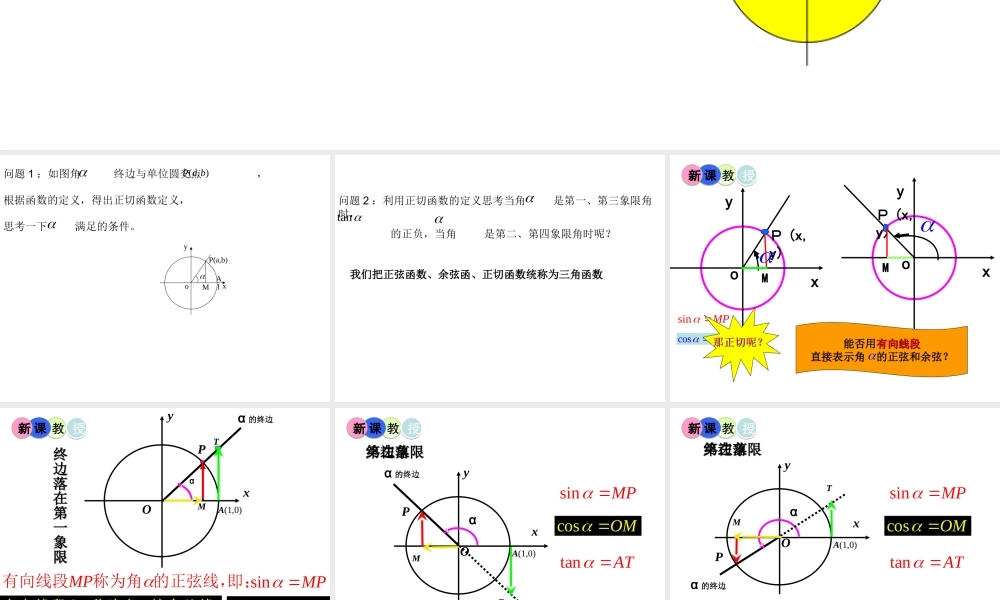
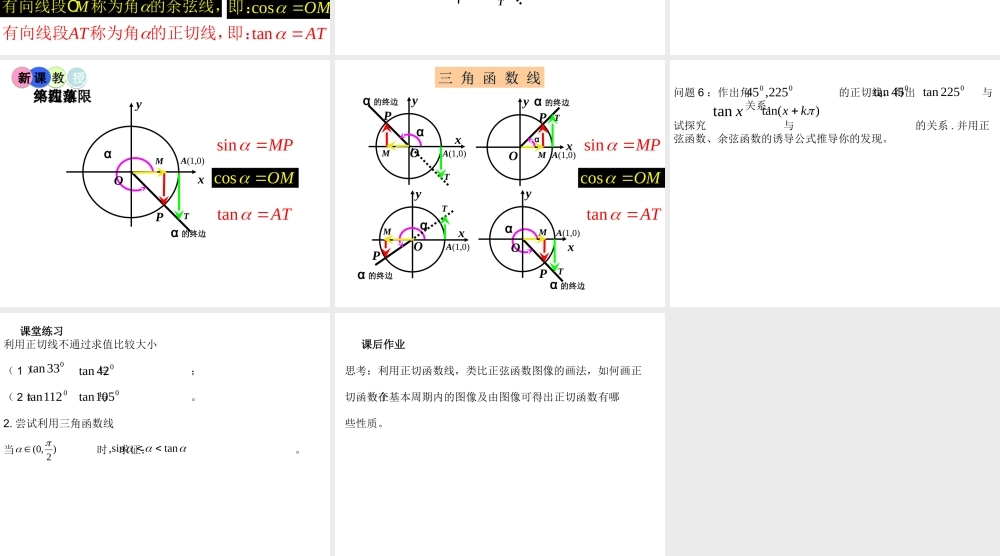
oyxPM AT 问题 1 :如图角 终边与单位圆交点 ,根据函数的定义,得出正切函数定义,思考一下 满足的条件。),(baPxyMoP(a,b)A1 问题 2 :利用正切函数的定义思考当角 是第一、第三象限角时, 的正负,当角 是第二、第四象限角时呢?tan我们把正弦函数、余弦函、正切函数统称为三角函数 P (x,y)xyoP (x,y)xyoMM教教 授授课课新新能否用有向线段有向线段直接表示角 的正弦和余弦?sinMP cosOM 那正切呢?那正切呢? α 的终边αOyxA(1,0)PMTsinMP 即:cosOM 即:tanAT 即:MP有向线段称为角 的正弦线,M有向线段O 称为角 的余弦线,AT有向线段称为角 的正切线,教教 授授课课新新终边落在第一象限终边落在第一象限 α 的终边αyxA(1,0)OPMTsinMP cosOM tanAT 终边落在第二象限终边落在第二象限教教 授授课课新新 α 的终边αyxA(1,0)OPMTsinMP cosOM tanAT 终边落在第三象限终边落在第三象限教教 授授课课新新 α 的终边αyxA(1,0)POMTsinMP cosOM tanAT 终边落在第四象限终边落在第四象限教教 授授课课新新 α 的终边αyxA(1,0)POα 的终边αyxA(1,0)O三 角 函 数 线三 角 函 数 线α 的终边αOyxA(1,0)PMTPMTα 的终边αyxA(1,0)OPMTMTsinMP cosOM tanAT 问题 6 :作出角 的正切线,得出 与 关系,试探究 与 的关系 . 并用正弦函数、余弦函数的诱导公式推导你的发现。00 225,45045tan0225tanxtan)tan(kx 课堂练习利用正切线不通过求值比较大小( 1 ) 与 ;( 2 ) 与 。2. 尝试利用三角函数线当 时,求证: 。033tan042tan0112tan0105tan)2,0( tansin 课后作业思考:利用正切函数线,类比正弦函数图像的画法,如何画正切函数在一个基本周期内的图像及由图像可得出正切函数有哪些性质。