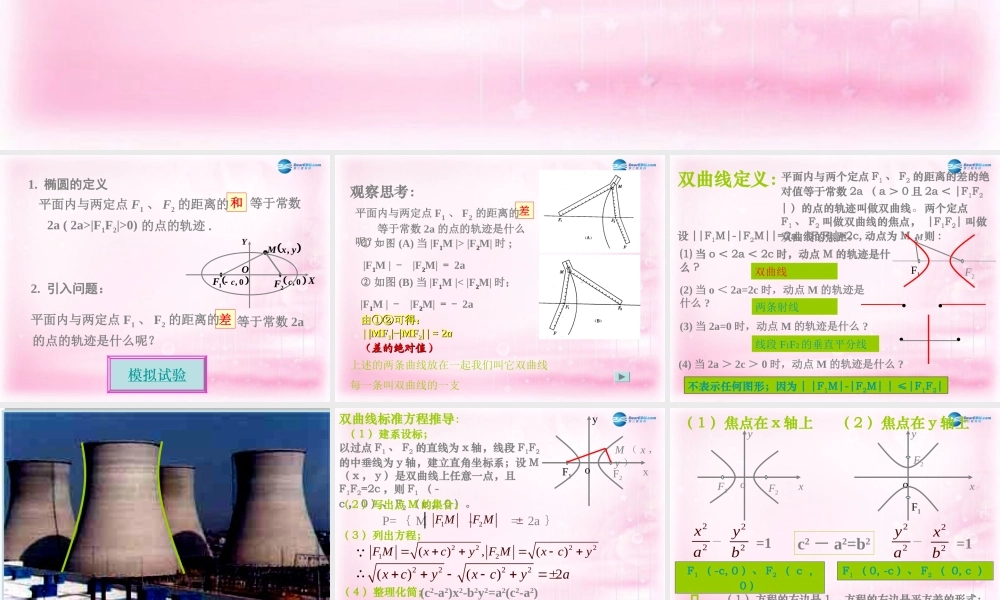
双曲线及其标准方程 1. 椭圆的定义和 等于常数2a ( 2a>|F1F2|>0) 的点的轨迹 .平面内与两定点 F1 、 F2 的距离的1F2F0,c0,cXYOyxM,2. 引入问题:差 等于常数 2a的点的轨迹是什么呢?平面内与两定点 F1 、 F2 的距离的模拟试验 观察思考:② 如图 (B) 当 |F11M |< |F22M| 时;|F11M | - |F22M| =- 2a ① 如图 (A) 当 |F11M |> |F22M| 时 ; |F11M | - |F22M| = 2a差平面内与两定点 F1 、 F2 的距离的 等于常数 2a 的点的轨迹是什么呢?上述的两条曲线放在一起我们叫它双曲线每一条叫双曲线的一支 由①②可得:由①②可得: | |MF| |MF11||--|MF|MF22| | = 2| | = 2aa ((差的绝对值)差的绝对值) 双曲线定义:平面内与两个定点 F1 、 F2 的距离的差的绝对值等于常数 2a ( a > 0 且 2a < |F1F2| )的点的轨迹叫做双曲线。两个定点F1 、 F2 叫做双曲线的焦点, |F1F2| 叫做双曲线的焦距。设 ||F1M|-|F2M||=2a, |F1F2|=2c, 动点为 M ,则 :不表示任何图形;因为 | |F1M|-|F2M| | ≤|F1F2|(1) 当 o < 2a < 2c 时,动点 M 的轨迹是什么 ?(2) 当 o < 2a=2c 时,动点 M 的轨迹是什么 ?(4) 当 2a > 2c > 0 时,动点 M 的轨迹是什么 ?(3) 当 2a=0 时,动点 M 的轨迹是什么 ?双曲线两条射线线段 F1F2 的垂直平分线 F1F2M F1F2xoy双曲线标准方程推导:( 1 )建系设标;M ( x ,y )以过点 F1 、 F2 的直线为 x 轴,线段 F1F2的中垂线为 y 轴,建立直角坐标系;设 M( x , y )是双曲线上任意一点,且F1F2=2c ,则 F1 ( -c , 0 )、 F2 ( c , 0 )。( 2 )写出点 M 的集合; P= { M - = 2a }2F M1F M( 3 )列出方程;( 4 )整理化简;(c2-a2)x2-b2y2=a2(c2-a2)令 c2-a2=b2双曲线标准方程:-22xa22yb=1 ( a > 0 , b >0 )222212(),()F MxcyF Mxcy 2222()()2xcyxcya∴ F1F2oxyF1F2oxy( 1 )焦点在 x 轴上( 2 )焦点在 y 轴上-22xa22yb=1-22ya22xb=1F1 ( -c, 0 )、 F2 ( c , 0 )F1 ( 0, -c )、 F2 ( 0, c )特特( 1 )方程的右边是 1 ,方程的左边是平方差的形式;( 2 )双曲线的焦点所在的坐标轴与方程左边正项的分 子相对应...