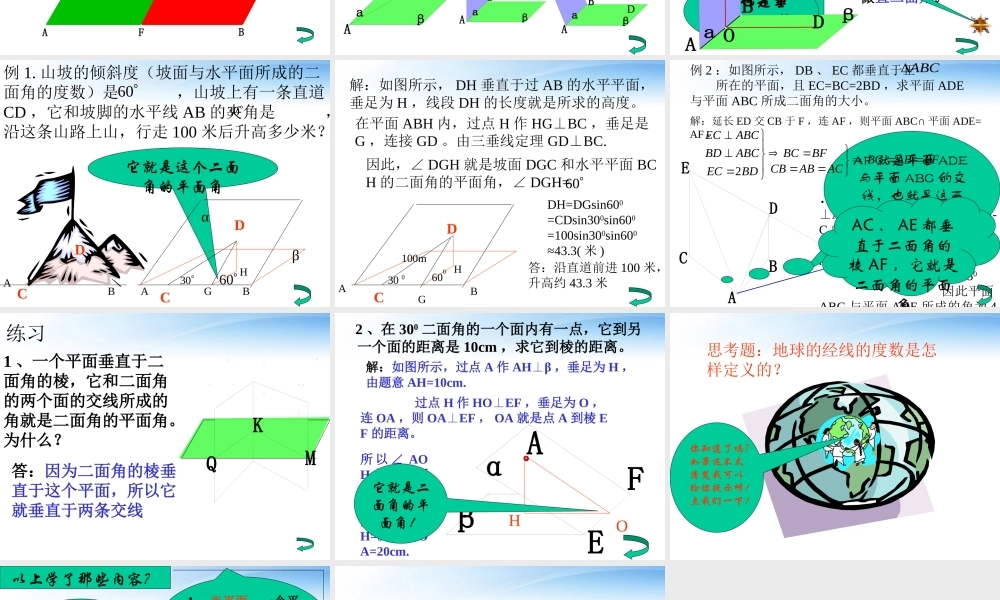
二面角 2二面角 2目录• 引入• 基本概念• 图形• 范例• 练习• 小结• 作业基本概念:1 、半平面:一个平面内的一条直线,把这个平面分成两部分,其中的每一部分都叫做半平面。ABCDEF2 、二面角:从一条直线出发的两个半平面所组成的图形叫做二面角。αaβBAβaαAB记为:二面角 α-AB-β或者二面角 α-a-β或者二面角 C-AB-DαβaBA这条直线叫做二面角的棱。这两个半平面叫做二面角的面。aβαABCD3 、二面角的平面角:以二面角的棱上的任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。4 、直二面角:平面角是直角的二面角叫做直二面角。αβEFOCDOC 是垂直于EF 的射线OD 也是垂直于 EF 的射线想知道二面角的大小是如何变化的吗?点我以下呀!aβαABODC∠COD= 90�0例 1. 山坡的倾斜度(坡面与水平面所成的二面角的度数)是 ,山坡上有一条直道CD ,它和坡脚的水平线 AB 的夹角是 ,沿这条山路上山,行走 100 米后升高多少米?603060ACDBHG它就是这个二面角的平面角30αβDCAB解:如图所示, DH 垂直于过 AB 的水平平面,垂足为 H ,线段 DH 的长度就是所求的高度。在平面 ABH 内,过点 H 作 HGBC⊥,垂足是G ,连接 GD 。由三垂线定理 GDBC.⊥因此,∠ DGH 就是坡面 DGC 和水平平面 BCH 的二面角的平面角,∠ DGH= 60DH=DGsin600=CDsin300sin600=100sin300sin600≈43.3( 米 )答:沿直道前进 100 米,升高约 43.3 米HGABDC306000100m例 2 :如图所示, DB 、 EC 都垂直于正 所在的平面,且 EC=BC=2BD ,求平面 ADE与平面 ABC 所成二面角的大小。 ABCECABDF解:延长 ED 交 CB 于 F ,连 AF ,则平面 ABC∩ 平面 ADE=AF ,∴∠CAF=900, 由三垂线定理 AEAF EAC⊥∴∠为二面角 E-AF-C 的平面角。在直角三角 形 ACE 中,AC=EC , ∴∠EAC=450 因此平面ABC 与平面 ADE 所成的角为 450.AF 就是平面 ADE与平面 ABC 的交线,也就是这两个平面所成的二面角的棱AC 、 AE 都垂直于二面角的棱 AF ,它就是二面角的平面角BFABBCACABCBBFBCBDECABCBDABCEC2练习1 、一个平面垂直于二面角的棱,它和二面角的两个面的交线所成的角就是二面角的平面角。为什么?答:因为二面角的棱垂直于这个平面,所以它就垂直于两条交线MKQ2 、在 300 二面...