函数的单调性-(2)VIP免费

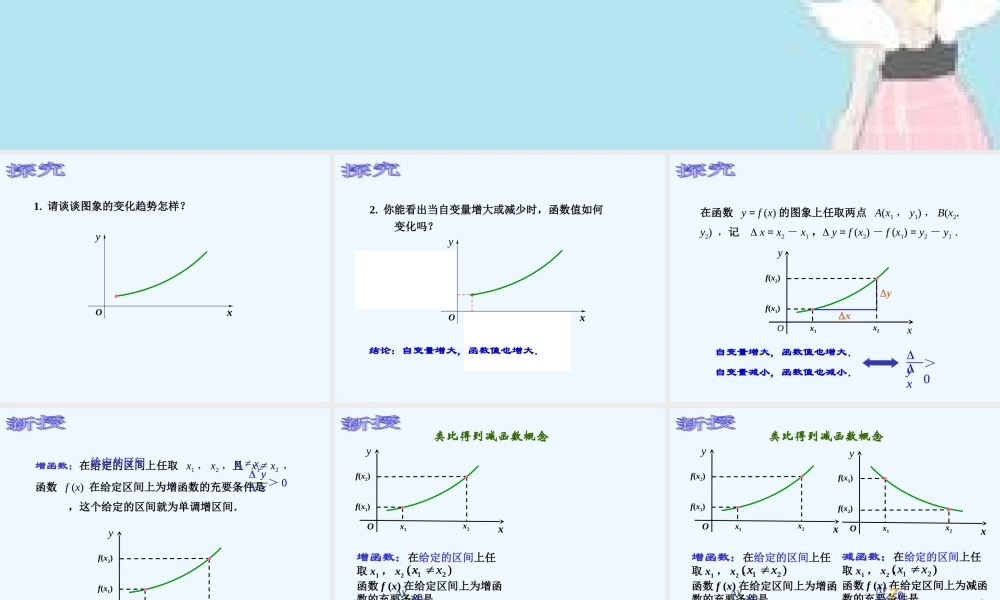
函数的单调性1. 请谈谈图象的变化趋势怎样？OxyOxy2. 你能看出当自变量增大或减少时，函数值如何 变化吗？结论：自变量增大，函数值也增大．在函数 y = f (x) 的图象上任取两点 A(x1 ， y1) ， B(x2, y2) ，记  x = x2 － x1 ， y = f (x2) － f (x1) = y2 － y1 ．自变量增大，函数值也增大．自变量减小，函数值也减小．xy Oxyx1x2f(x1)f(x2)xy＞0增函数：在给定的区间上任取 x1 ， x2 ，且 x1 ≠ x2 ，函数 f (x) 在给定区间上为增函数的充要条件是 ，这个给定的区间就为单调增区间．xy ＞ 0Oxyx1x2f(x1)f(x2)给定的区间 x1 ≠ x2 xy ＞ 0Oxyx1x2f(x1)f(x2)增函数：在给定的区间上任取 x1 ， x2 ， 函数 f (x) 在给定区间上为增函数的充要条件是 ，这个给定的区间就为单调增区间。)(21xx xy>0)(21xx xy>0类比得到减函数概念减函数：在给定的区间上任取 x1 ， x2 ， 函数 f (x) 在给定区间上为减函数的充要条件是 ，这个给定的区间就为单调减区间。)(21xx )(21xx Oxyx1x2f(x2)f(x1)xy<0类比得到减函数概念Oxyx1x2f(x1)f(x2)增函数：在给定的区间上任取 x1 ， x2 ， 函数 f (x) 在给定区间上为增函数的充要条件是 ，这个给定的区间就为单调增区间。)(21xx xy>0)(21xx xy>0例 1 给出函数 y = f (x) 的图象，如图所示，根据图象说出这个函数在哪些区间上是增函数？哪些区间上是减函数？解：函数在区间 [-1 ， 0] ， [2 ， 3] 上是减函数； 在区间 [0 ， 1] ， [3 ， 4] 上是增函数．23x14-1Oy（ 2 ）观察教材 P 64 ，例 2 的函数图象，分别说出函数在 ( －∞， 0) 和 (0 ，＋∞ ) 上是增函数还是减函数． （ 1 ）观察教材 P 64 ，例 1 的函数图象，说出函数在 ( －∞，＋∞ ) 上是增函数还是减函数．Oxyx1x2f(x2)f(x1)怎样利用函数解析式判断单调性Oxyx1x2f(x1)f(x2)减函数增函数y=f(x)自变量增大 (x>0)函数值增大 (y>0)自变量增大 (x>0)函数值减小 (y<0)0xy0xyy=f(x)例 2 证明函数 f(x) = 3 x ＋ 2 在区间 ( －∞， +∞) 上是 增函数．证明：设 x1 ， x2 是任意两个不相等的实数，则y = f(x2) － f(x1) = (3x2+2) － (3x1+2) = 3(x2 － x1)因此，函数 f(x) ＝ 3 x ...