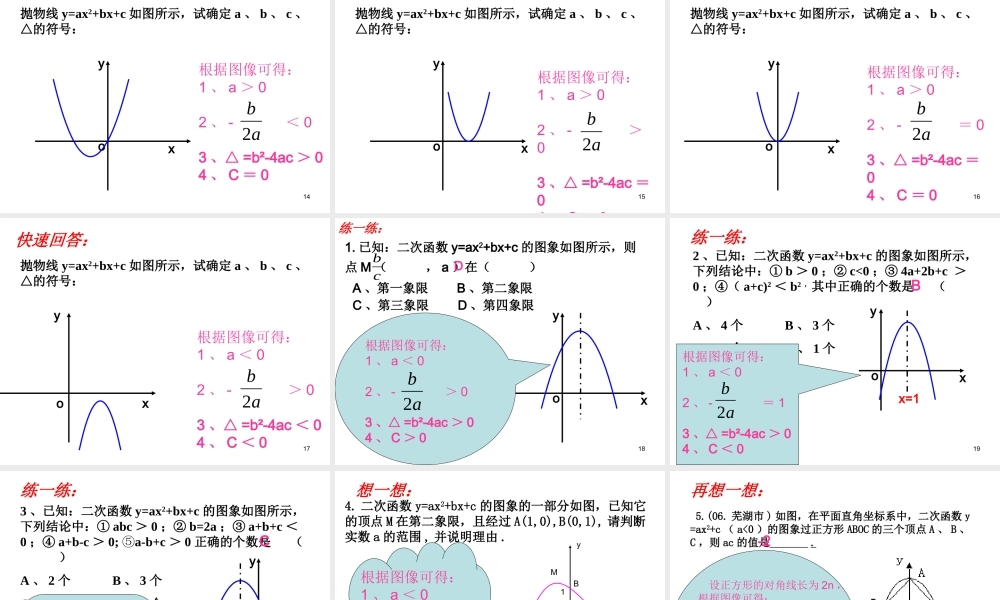
1二次函数中的符号问题X 2 3二次函数中的符号问题 4 5 6 7回味知识点:1 、抛物线 y=ax2+bx+c 的开口方向与什么有关?2 、抛物线 y=ax2+bx+c 与 y 轴的交点是 .3 、抛物线 y=ax2+bx+c 的对称轴是 .a > 0 时,开口向上; a < 0 时,开口向下。( 0 、 c )X=- ab2 8归纳知识点:抛物线 y=ax2+bx+c 的符号问题:( 1 ) a 的符号:由抛物线的开口方向确定开口向上a>0开口向下a<0( 2 ) C 的符号:由抛物线与 y 轴的交点位置确定 :交点在 x 轴上方c>0交点在 x 轴下方c<0经过坐标原点c=0 9( 3 ) b 的符号:由对称轴的位置确定:对称轴在 y 轴左侧a 、 b 同号对称轴在 y 轴右侧a 、 b 异号对称轴是 y 轴b=0( 4 ) b2-4ac 的符号:由抛物线与 x 轴的交点个数确定 :与 x 轴有两个交点b2-4ac>0与 x 轴有一个交点b2-4ac=0与 x 轴无交点b2-4ac<0归纳知识点:简记为:左同右异 10归纳知识点:抛物线 y=ax2+bx+c 的符号问题:( 5 ) a+b+c 的符号:由 x=1 时抛物线上的点的位置确定( 6 ) a-b+c 的符号:由 x=-1 时抛物线上的点的位置确定 1111归纳知识点:抛物线 y=ax2+bx+c 的符号问题:( 5 ) a+b+c 的符号:由 x=1 时抛物线上的点的位置确定( 6 ) a-b+c 的符号:由 x=-1 时抛物线上的点的位置确定你还可想到啥? 1212利用以上知识主要解决以下几方面问题:( 1 )由 a,b,c,∆ 的符号确定抛物线在坐标系中的 大 致位置;( 2 )由抛物线的位置确定系数 a,b,c,∆ 等符号及有关 a,b,c 的代数式的符号; 13快速回答:抛物线 y=ax2+bx+c 如图所示,试确定 a 、 b 、 c 、△的符号:xoy根据图像可得:1 、 a > 02 、 - > 03 、△ =b²-4ac > 04 、 C > 0ab2 14抛物线 y=ax2+bx+c 如图所示,试确定 a 、 b 、 c 、△的符号:xyo快速回答:根据图像可得:1 、 a > 02 、 - < 03 、△ =b²-4ac > 04 、 C = 0ab2 15抛物线 y=ax2+bx+c 如图所示,试确定 a 、 b 、 c 、△的符号:xyo快速回答:ab2根据图像可得:1 、 a > 02 、 - >03 、△ =b²-4ac =04 、 C > 0 16抛物线 y=ax2+bx+c 如图所示,试确定 a 、 b 、 c 、△的符号:xyo快速回答:根据图像可得:1 、 a > 02 、 - = 03 、△ =b²-4ac =04 、 C...