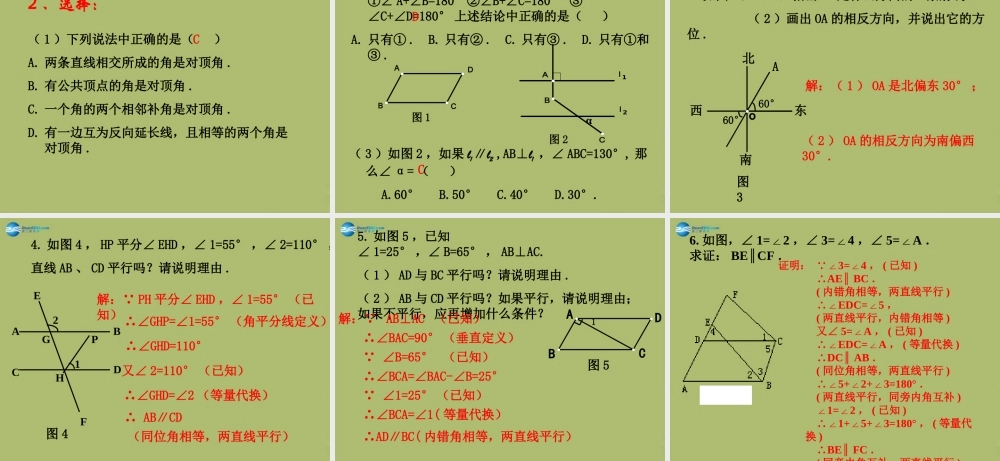
第二章 相交线与平行线丰富情境实际问题 相交线与 平行线相交线平行线尺规作图——作一条线段等于已知线段、作一个角等于已知角 .以及简单应用 .相交线补角余角对顶角 如果两个角的和是平角(或 180° ),称这两个角互为补角 .同角或等角的补角相等 .性质:EFDA21 像上图中具有∠ 1 与∠ 2 这样位置关系的两个角就称它们互为邻补角 .注:注:互为补角只反映大小关系,不反映位置关系 .而互为邻补角既反映大小关系,又反映位置关系 . 如果两个角的和是直角(或 90° ),称这两个角互为余角 .同角或等角的余角相等 .性质:注:注:互为余角只反映大小关系,不反映位置关系 .12ADCBO 如图,直线 AB 与直线 CD 相交于点 O ,∠ 1 与∠ 2 有公共顶点 O ,它们的两边互为反向延长线,这样的两个角叫做对顶角 .对顶角相等 . 性质:注:注:对顶角既反映大小关系,又反映位置关系 .平行线探索直线平行的条件探索直线平行的特征图中识概念 :“F” 型中的同位角 “Z” 字型中的内错角 “U” 字型中的同旁内角 ( 2 )同位角相等,两直线平行 .( 1 )平行线定义;( 3 )内错角相等,两直线平行 .( 4 )同旁内角互补,两直线平行 .( 5 )如果两条直线都和第三条直线平行,那么这 两条直线也平行 .注:同位角,内错角,同旁内角均不是平行线所特有的 . 它们只反映角的位置关系,而不反映大小关系 .两直线平行的条件:( 1 )两直线平行,同位角相等 .( 2 )两直线平行,内错角相等 .( 3 )两直线平行,同旁内角互补 .平行线的 3 个特征:1 、判断:( 1 )两条不平行的线段,在同一平面内必相交 .( )( 2 )两条直线被第三条直线所截,内错角相等 .( )( 3 )相等的两个角为对顶角 .( )( 4 )两条直线相交,如果有两个角相等,那么这两个角是对顶角 .( )( 5 )两条直线被第三条直线所截,如果同位角相等,那么同旁内角互补 .( )××××√( 6 )两条直线相交后,只有两对对顶角和一组邻补角,一组互余的角. ( )×2 、选择:( 1 )下列说法中正确的是( )A. 两条直线相交所成的角是对顶角 .B. 有公共顶点的角是对顶角 .C. 一个角的两个相邻补角是对顶角 .D. 有一边互为反向延长线,且相等的两个角是对顶角 .C( 2 )如图 1 ,如果 AD∥BC, 则有①∠ A+∠B=180°②∠B+∠C=180° ③ ∠C+∠D=180° 上述...