数学 1.1.1正弦定理课件4 新人教A版必修5 课件VIP免费

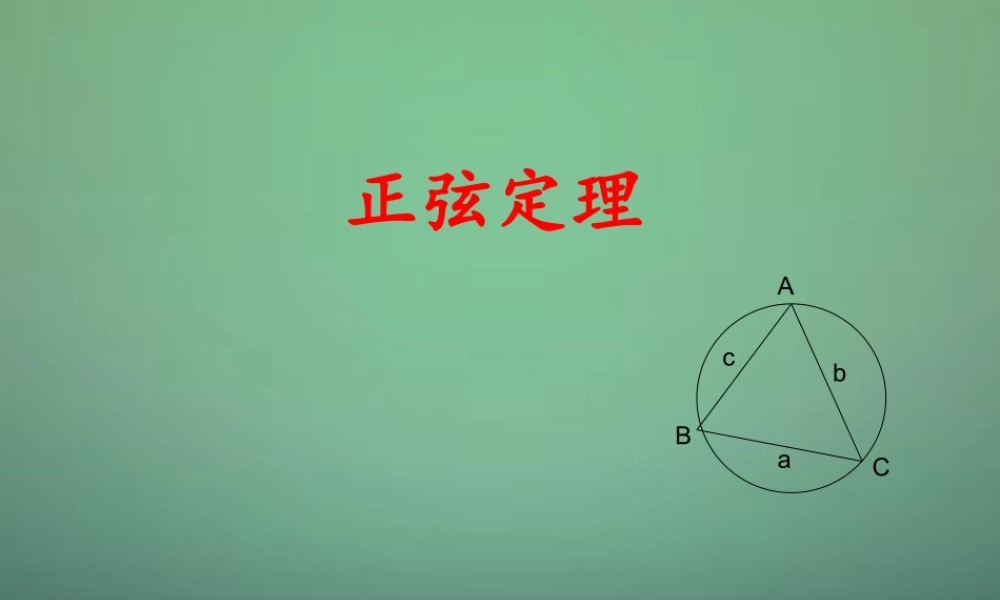
正弦定理AbaCBc正弦定理问题 1 ：我们已经学习过任意三角形的哪些边角关系？三角形内角和为 180 度；大边对大角，小边对小角；直角三角形满足勾股定理 .问题 2 ：我们能否得到三角形边角关系准确量化的表示？CcBbAasinsinsin思考：怎样证明该式子成立？，则的对边分别是中，角在cbaCBAABC,,,,我们先研究直角三角形的情况bCaAcB1sin,sin,sinCcbBcaAABCRt可知：中，由正弦函数的定义在BbcAacsin,sin所以，BbAasinsin即，CcBbAasinsinsin所以：上述等式对于任意三角形都成立吗？正弦定理锐角三角形ABCabcD.DBCADA，垂足为作过BcADABDRtsin中，在CbADACDRtsin中，在CbBcsinsin所以，CcBbsinsin即：.EACBEB，垂足为作同理，过CcAasinsin可得：ECcBbAasinsinsin综上：正弦定理钝角三角形ACBacbD正弦定理：在一个三角形中，各边与它所对角的正弦的比相等，即CcBbAasinsinsin正弦定理正弦定理可以解决哪些三角形的问题？1. 已知两角和任意一边，求其他两边和一角；2. 已知两边和其中一边的对角，求其他的边和角 .D.3 C.2 3B. 2.A) (60,45,3100BCCAABABC，则中，：在例A 235D. 365C. 364B. 36.A) (75,45,5100aCAbABC，则中，若：在变式C正弦定理.4,2,32，解这个三角形中，：在例BbaABC23sin4sin2sin3sinsinAABbAa可得解：由0012060 或ABAba226756000cCA，时，当2261512000cCA，时，当注意：用正弦定理求角时，可能出现两解的情况，需根据“大边对大角”进行判断 .正弦定理060,45 )2(43,2312AbaBbaABC，，）（解得个数：中，根据下列条件指出：在变式无解有一解正弦定理在正弦定理中，比值等于什么？AbaCBcDCDBDB，连接作三角形外接圆的直径过点RBDCaRaBDBCBDCBCDRt2sin2sin即中，在RAaBDCBAC2sin 即又是三角形外接圆半径）（RRCcBbAa2sinsinsin正弦定理是三角形外接圆半径）（RRCcBbAa2sinsinsin正弦定理的变形式CRcBRbARasin2sin2sin2RcCRbBRaA2sin2sin2sin正弦定理以上选项均不正确等腰或直角三角形直角三角形等腰三角形则该三角形是中，如果：在例D. C. B. .A) (,coscos3BbAaABC.,coscoscos3试判断三角形的形状中，若：在变式cCbBaAABCCCRcBRbARasin2 sin2 sin2解：CRCBRBARAsin2cossin2cossin2cos原式...