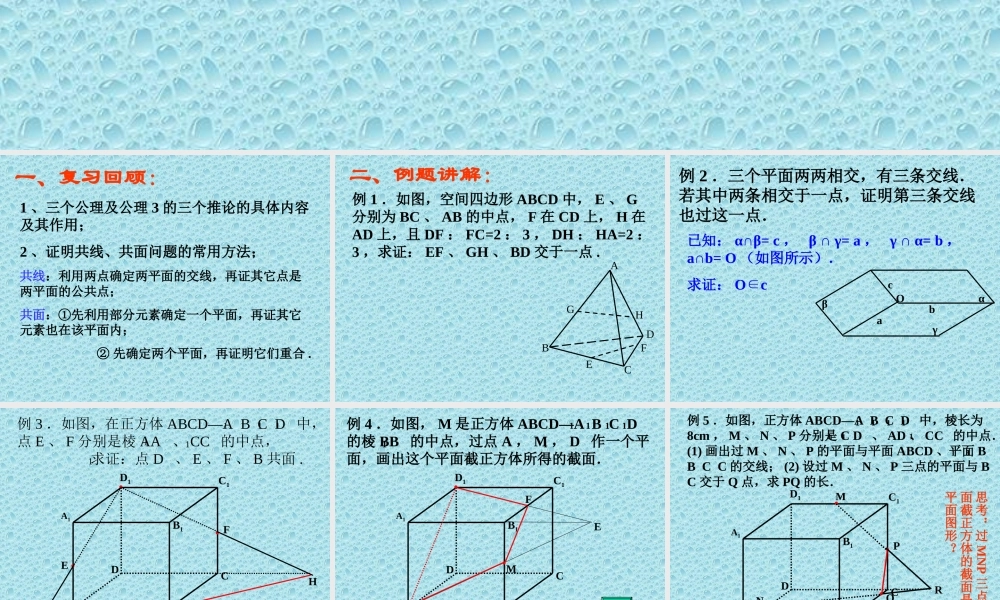
平面的基本性质应用 (2) 1 、三个公理及公理 3 的三个推论的具体内容及其作用;2 、证明共线、共面问题的常用方法;共线:利用两点确定两平面的交线,再证其它点是两平面的公共点;共面:①先利用部分元素确定一个平面,再证其它 元素也在该平面内; ② 先确定两个平面,再证明它们重合 .一、复习回顾: 二、例题讲解:例 1 .如图,空间四边形 ABCD 中, E 、 G分别为 BC 、 AB 的中点, F 在 CD 上, H 在AD 上,且 DF : FC=2 : 3 , DH : HA=2 :3 ,求证: EF 、 GH 、 BD 交于一点 .ABEHGDCF 例 2 .三个平面两两相交,有三条交线.若其中两条相交于一点,证明第三条交线也过这一点.αγβOcba已知: α∩β= c , β ∩ γ= a , γ ∩ α= b , a∩b= O (如图所示).求证: Oc∈ ABCDA1B1C1D1EF例 3 .如图,在正方体 ABCD—A B C D 中,点 E 、 F 分别是棱 AA 、 CC 的中点, 求证:点 D 、 E 、 F 、 B 共面 .1111111GH 例 4 .如图, M 是正方体 ABCD—A B C D 的棱 BB 的中点,过点 A , M , D 作一个平面,画出这个平面截正方体所得的截面.111111ABCDA1B1C1D1MEF ABCDA1B1C1D1QPM例 5 .如图,正方体 ABCD—A B C D 中,棱长为8cm , M 、 N 、 P 分别是 C D 、 AD 、 CC 的中点.(1) 画出过 M 、 N 、 P 的平面与平面 ABCD 、平面 BB C C 的交线; (2) 设过 M 、 N 、 P 三点的平面与 BC 交于 Q 点,求 PQ 的长.111111111NR思考:过MNP三点的平面截正方体的截面是什么平面图形? 三、课堂小结:1 、画出截面即找平面的交线;2 、证明问题包括: ① 点共线问题; ② 线共点问题; ③ 点、线共面问题 . 应注意总结各种问题的证明方法. 四、作业布置:补充三条