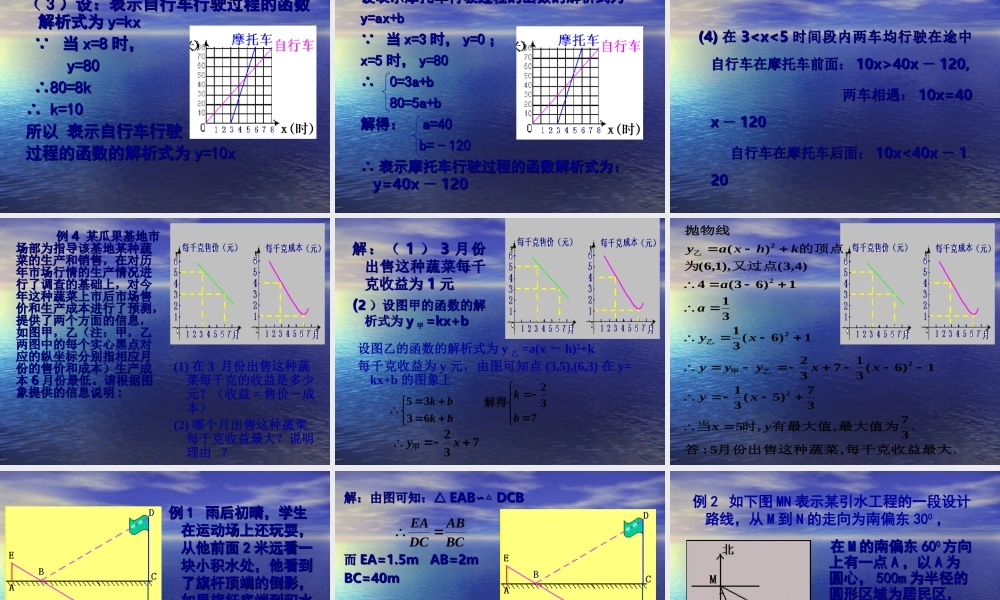
初中数学应用型综合问题( 第二讲) 应用型综合问题应用型综合问题代数知识的应用代数知识的应用几何知识的应用几何知识的应用11 、数与式的应用、数与式的应用22 、方程、方程 (( 组组 )) 的应用的应用33 、不等式、不等式 (( 组组 )) 的应的应用用44 、函数的应用、函数的应用平行线分线段成比平行线分线段成比例,相似三角形的例,相似三角形的性质,勾股定理,性质,勾股定理,三角函数及圆三角函数及圆 例例 11 :公路上有:公路上有 AA 、、 BB 、、 CC 三站,一辆汽三站,一辆汽车在上午车在上午 88 时从离时从离 AA 站站 1010 千米的千米的 PP 地出地出发向发向 CC 站匀速前进,站匀速前进, 1515 分钟后离分钟后离 AA 站站 2200 千米。千米。(1)(1) 设出发设出发 xx 小时后,汽车离小时后,汽车离 AA 站站 yy 千米,千米,写出写出 yy 与与 xx 之间的函数关系式。之间的函数关系式。(2)(2) 当汽车行驶到离当汽车行驶到离 AA 站站 150150 千米的千米的 BB 站站时,接到通知要在中午时,接到通知要在中午 1212 点前赶到离点前赶到离 BB站站 3030 千米的千米的 CC 站,汽车若按原速能否按站,汽车若按原速能否按时到达?若能是在几点几分,若不能,车时到达?若能是在几点几分,若不能,车速最少应提高到多少?速最少应提高到多少? 分析:根据已知可确定车速为分析:根据已知可确定车速为 4040 千千米米 // 时,故(时,故( 11 )便可解决:)便可解决: y=40y=40x+10,x+10, 由已知可知从由已知可知从 PP 地到地到 CC 站,站,须在须在 44 小时内走完,而实际这段路小时内走完,而实际这段路程需程需 4.254.25 小时,所以按原速度不能小时,所以按原速度不能按时到达;从按时到达;从 PP 地到地到 BB 站,用去时站,用去时间间 3.53.5 小时,故剩下的小时,故剩下的 3030 千米,必千米,必须在须在 0.50.5 小时内走完。小时内走完。 解解 : (1)y=40x+10: (1)y=40x+10 (2)(2) 当当 y=150+30=180(y=150+30=180( 千米)时,千米)时, 则汽车按原速不能按时到达。则汽车按原速不能按时到达。 当当 y=150y=150 (千米)时,(千米)时,设提速后车速为设提速后车速为 v,v, 则则 [(12-8)-3.5]v=30[(12-8)-3.5]v=30 v=60v=60 (千米(千米 // 时)时)答:车速应至少提高到答:车速应至少提高到 6060 千米千米 // 时,才能在...