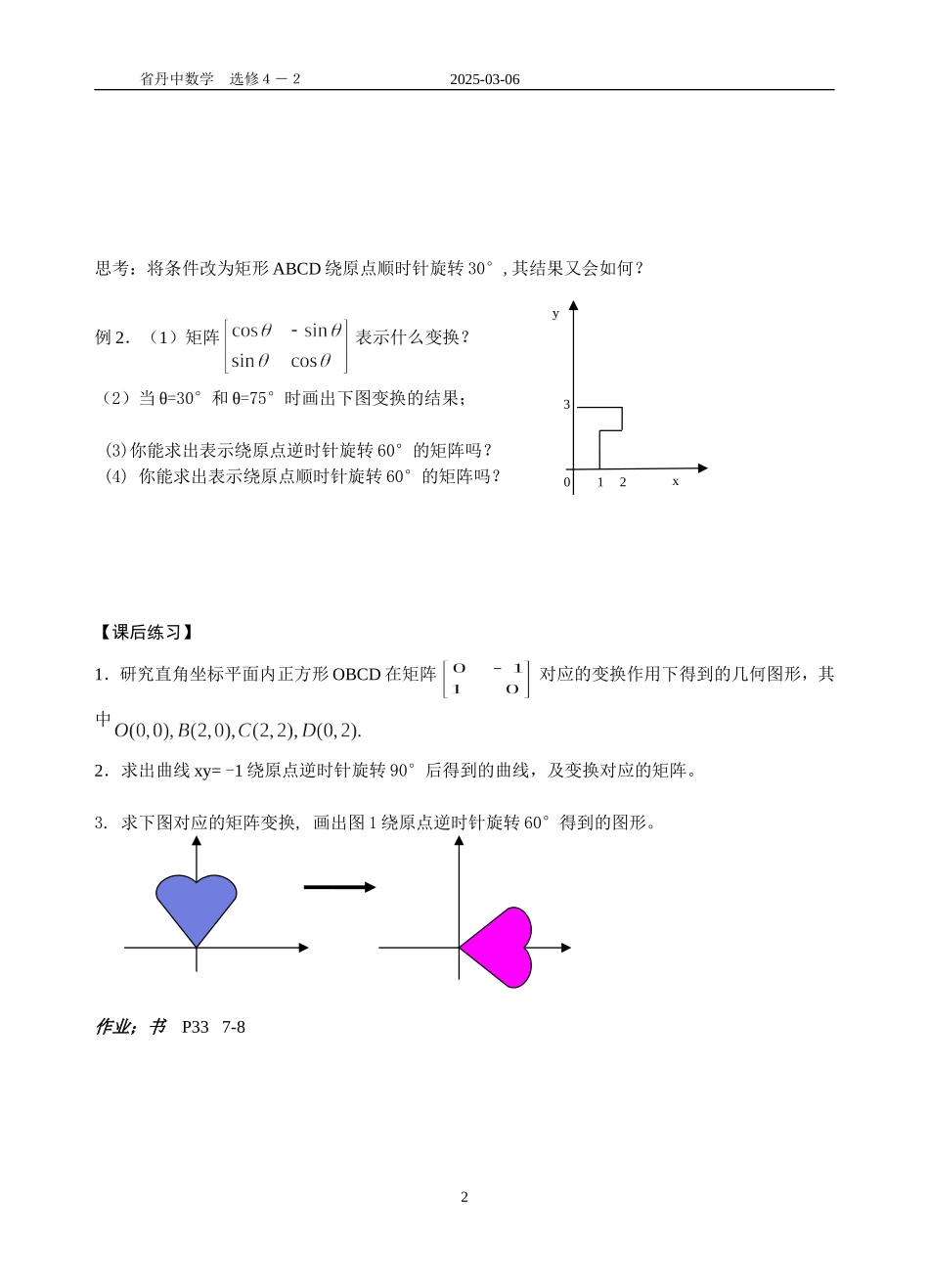
省丹中数学 选修4-2 2025-03-06课时 5 旋转变换【教学目标】1、掌握旋转变换的矩阵表示及其几何意义;2、从几何上理解二阶矩阵对应的变换是线形变换;3、会证明二阶矩阵对应的变换把直线变成变成直线,或者把直线变为点【教学过程】一、问题情境 如图所示,假设大风车的叶片在同一平面内转动,以旋转中心为坐标原点建立直角坐标系,已知大风车上一点 P(x,y),它绕 O 点逆时针旋转 θ 角到点 P’(x’,y’),点的位置变化可以看作一个几何变换,怎么用矩阵来刻画这一变换?不妨设 OP 与 x 轴交角为,,则有。又因为,故有 将上式展开,并将代入,有即 二、数学建构旋转变换矩阵和旋转变换矩阵通常叫做旋转变换矩阵,对应的变换称做旋转变换,其中的角叫做旋转角,点 O 叫做旋转中心。旋转变换只改变几何图形的相对位置,不会改变几何图形的形状。旋转中心在旋转过程中保持不变,图形的旋转由旋转中心和旋转的角度所决定。显然,绕定点作旋转的变换相当于关于定点作中心反射变换。三、例题讲解例1.已知,求矩形 ABCD 绕原点逆时针旋转后所得到的图形,并求出其顶点坐标,画出示意图1( , )P x y ( , )P x y0xy123省丹中数学 选修4-2 2025-03-06思考:将条件改为矩形 ABCD 绕原点顺时针旋转 30°,其结果又会如何?例 2.(1)矩阵表示什么变换?(2)当 θ=30°和 θ=75°时画出下图变换的结果; (3)你能求出表示绕原点逆时针旋转 60°的矩阵吗?(4) 你能求出表示绕原点顺时针旋转 60°的矩阵吗?【课后练习】1.研究直角坐标平面内正方形 OBCD 在矩阵对应的变换作用下得到的几何图形,其中2.求出曲线 xy= -1 绕原点逆时针旋转 90°后得到的曲线,及变换对应的矩阵。3. 求下图对应的矩阵变换, 画出图 1 绕原点逆时针旋转 60°得到的图形。作业;书 P33 7-82