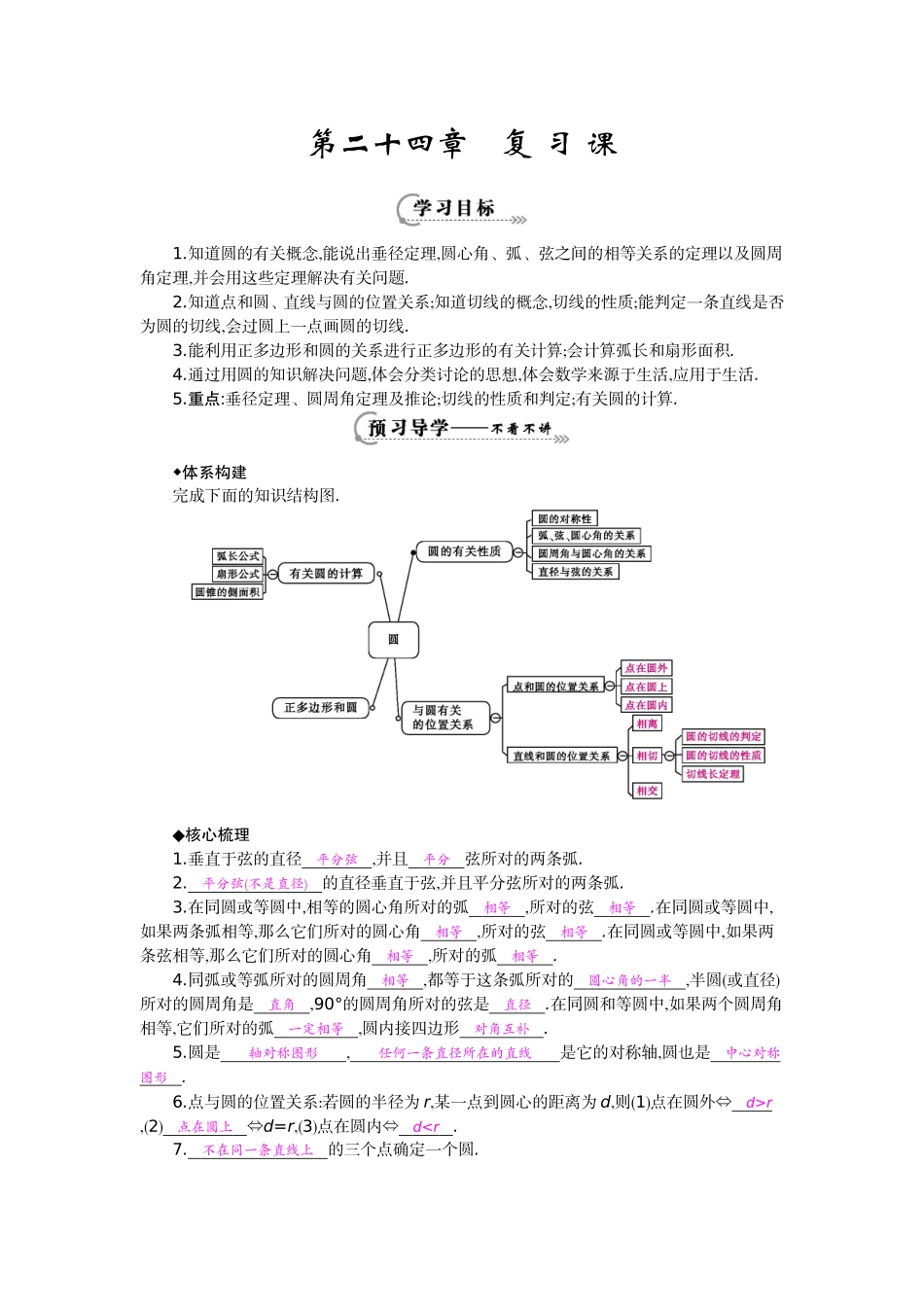
第二十四章 复 习 课 1.知道圆的有关概念,能说出垂径定理,圆心角、弧、弦之间的相等关系的定理以及圆周角定理,并会用这些定理解决有关问题.2.知道点和圆、直线与圆的位置关系;知道切线的概念,切线的性质;能判定一条直线是否为圆的切线,会过圆上一点画圆的切线.3.能利用正多边形和圆的关系进行正多边形的有关计算;会计算弧长和扇形面积.4.通过用圆的知识解决问题,体会分类讨论的思想,体会数学来源于生活,应用于生活.5.重点:垂径定理、圆周角定理及推论;切线的性质和判定;有关圆的计算. ◆体系构建完成下面的知识结构图.◆核心梳理1.垂直于弦的直径 平分弦 ,并且 平分 弦所对的两条弧. 2. 平分弦 ( 不是直径 ) 的直径垂直于弦,并且平分弦所对的两条弧. 3.在同圆或等圆中,相等的圆心角所对的弧 相等 ,所对的弦 相等 .在同圆或等圆中,如果两条弧相等,那么它们所对的圆心角 相等 ,所对的弦 相等 .在同圆或等圆中,如果两条弦相等,那么它们所对的圆心角 相等 ,所对的弧 相等 . 4.同弧或等弧所对的圆周角 相等 ,都等于这条弧所对的 圆心角的一半 ,半圆(或直径)所对的圆周角是 直角 ,90°的圆周角所对的弦是 直径 .在同圆和等圆中,如果两个圆周角相等,它们所对的弧 一定相等 ,圆内接四边形 对角互补 . 5.圆是 轴对称图形 , 任何一条直径所在的直线 是它的对称轴,圆也是 中心对称 图形 . 6.点与圆的位置关系:若圆的半径为 r,某一点到圆心的距离为 d,则(1)点在圆外⇔ d>r ,(2) 点在圆上 ⇔d=r,(3)点在圆内⇔ dr. 9.切线的判定定理: 经过半径的外端并且垂直于这条半径 的直线是圆的切线. 切线的性质定理:圆的切线 垂直于经过切点的半径 . 10.弧长 l= (n 为圆心角度数,R 为扇形半径). 11.S 扇形= = lR (n 为圆心角度数,R 为半径,l 为弧长). 12.S 锥侧= π rl (r 为圆锥底面圆的半径,l 为圆锥的母线). 专题一:垂径定理及推论1.如图,☉O 的半径为 5,弦 AB 的长为 8,M 是弦 AB 上的动点,则线段 OM 长的最小值为(B)A.2 B.3 C.4 D.52.如图,已知 AB 是☉O 的直径,CD⊥AB,垂足为点 E,如果 BE=OE,AB=10 cm,求△ACD 的周长.解:...