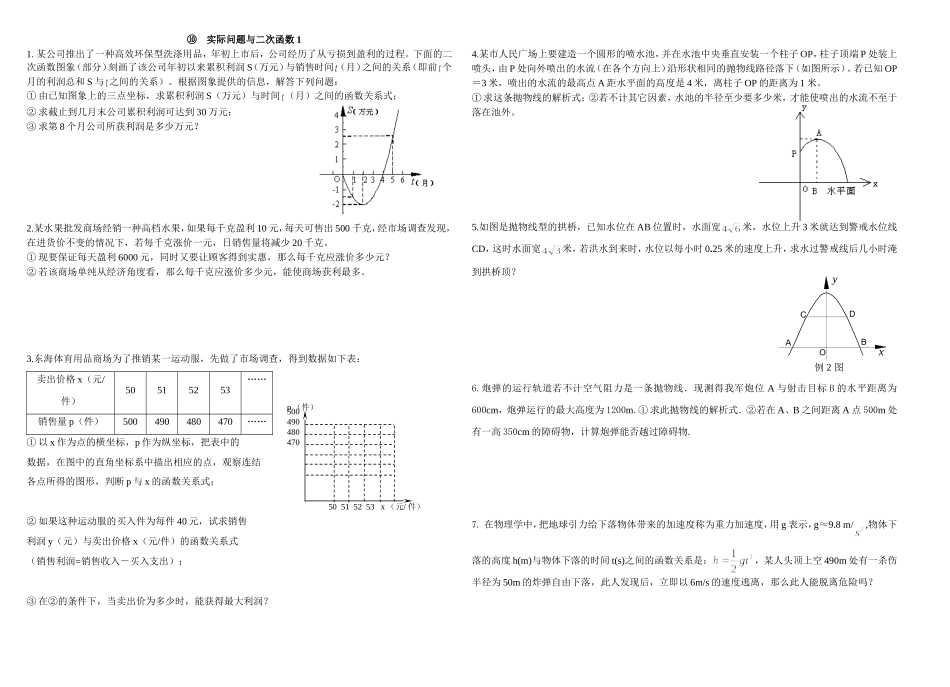
⑩ 实际问题与二次函数 11. 某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程。下面的二次函数图象(部分)刻画了该公司年初以来累积利润 S(万元)与销售时间 (月)之间的关系(即前 个月的利润总和 S 与 之间的关系)。根据图象提供的信息,解答下列问题: ① 由已知图象上的三点坐标,求累积利润 S(万元)与时间 (月)之间的函数关系式;② 求截止到几月末公司累积利润可达到 30 万元;③ 求第 8 个月公司所获利润是多少万元? 2.某水果批发商场经销一种高档水果,如果每千克盈利 10 元,每天可售出 500 千克,经市场调查发现,在进货价不变的情况下,若每千克涨价一元,日销售量将减少 20 千克。① 现要保证每天盈利 6000 元,同时又要让顾客得到实惠,那么每千克应涨价多少元?② 若该商场单纯从经济角度看,那么每千克应涨价多少元,能使商场获利最多。3.东海体育用品商场为了推销某一运动服,先做了市场调查,得到数据如下表: 卖出价格 x(元/件)50515253……销售量 p(件)500490480470……① 以 x 作为点的横坐标,p 作为纵坐标,把表中的数据,在图中的直角坐标系中描出相应的点,观察连结各点所得的图形,判断 p 与 x 的函数关系式;② 如果这种运动服的买入件为每件 40 元,试求销售利润 y(元)与卖出价格 x(元/件)的函数关系式(销售利润=销售收入-买入支出);③ 在②的条件下,当卖出价为多少时,能获得最大利润?4.某市人民广场上要建造一个圆形的喷水池,并在水池中央垂直安装一个柱子 OP,柱子顶端 P 处装上喷头,由 P 处向外喷出的水流(在各个方向上)沿形状相同的抛物线路径落下(如图所示)。若已知 OP=3 米,喷出的水流的最高点 A 距水平面的高度是 4 米,离柱子 OP 的距离为 1 米。① 求这条抛物线的解析式;②若不计其它因素,水池的半径至少要多少米,才能使喷出的水流不至于落在池外。5.如图是抛物线型的拱桥,已知水位在 AB 位置时,水面宽米,水位上升 3 米就达到警戒水位线CD,这时水面宽米,若洪水到来时,水位以每小时 0.25 米的速度上升,求水过警戒线后几小时淹到拱桥顶?6.炮弹的运行轨道若不计空气阻力是一条抛物线.现测得我军炮位 A 与射击目标 B 的水平距离为600cm,炮弹运行的最大高度为 1200m.① 求此抛物线的解析式.②若在 A、B 之间距离 A 点 500m 处有一高 350cm 的障...