函数的表示法二VIP免费

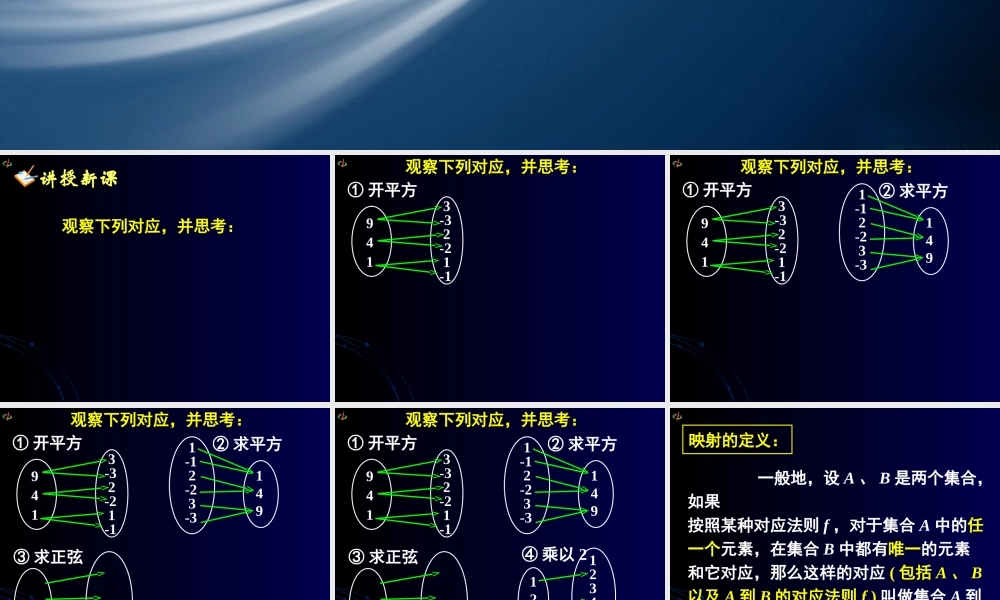
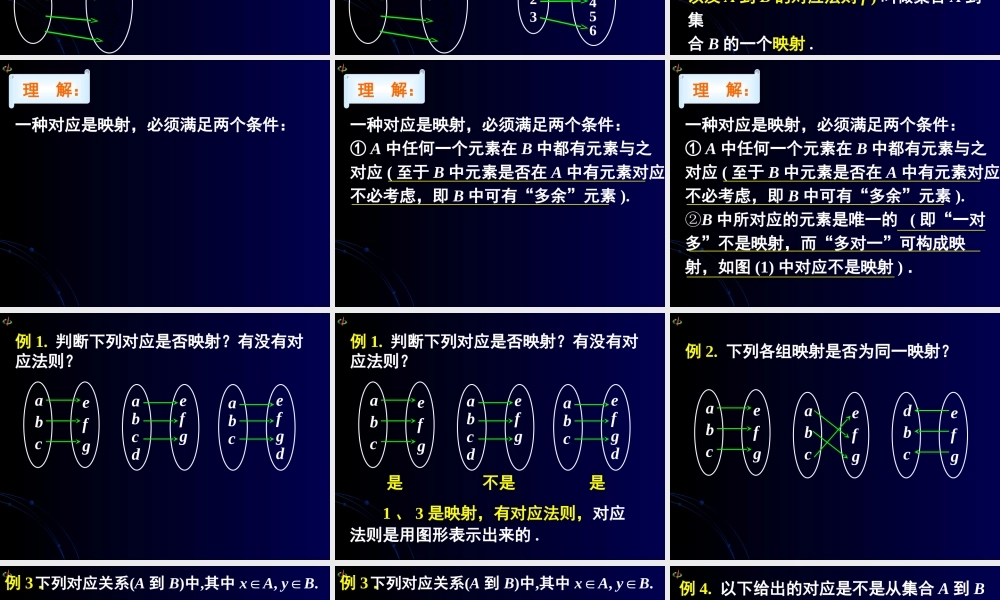
观察下列对应，并思考：讲授新课① 开平方观察下列对应，并思考：941 3-3 2-2 1-1① 开平方 1-1 2-2 3-3149② 求平方 观察下列对应，并思考：941 3-3 2-2 1-1① 开平方③ 求正弦 1-1 2-2 3-3149② 求平方 观察下列对应，并思考：941 3-3 2-2 1-1906045301232221① 开平方③ 求正弦 906045301232221④ 乘以 2 123123456 1-1 2-2 3-3149② 求平方 观察下列对应，并思考：941 3-3 2-2 1-1 一般地，设 A 、 B 是两个集合，如果按照某种对应法则 f ，对于集合 A 中的任一个元素，在集合 B 中都有唯一的元素和它对应，那么这样的对应 ( 包括 A 、 B以及 A 到 B 的对应法则 f ) 叫做集合 A 到集合 B 的一个映射 .映射的定义：一种对应是映射，必须满足两个条件：理 解：一种对应是映射，必须满足两个条件：① A 中任何一个元素在 B 中都有元素与之对应 ( 至于 B 中元素是否在 A 中有元素对应不必考虑，即 B 中可有“多余”元素 ). 理 解：一种对应是映射，必须满足两个条件：① A 中任何一个元素在 B 中都有元素与之对应 ( 至于 B 中元素是否在 A 中有元素对应不必考虑，即 B 中可有“多余”元素 ). ②B 中所对应的元素是唯一的 ( 即“一对多”不是映射，而“多对一”可构成映射，如图 (1) 中对应不是映射 ) ．理 解：例 1. 判断下列对应是否映射？有没有对应法则？abcefgabcdefgabcefgd例 1. 判断下列对应是否映射？有没有对应法则？abcefgabcdefg是不是是 1 、 3 是映射，有对应法则，对应法则是用图形表示出来的 .abcefgd例 2. 下列各组映射是否为同一映射？abcefgabcefgdbcefg下列对应关系(A 到 B)中,其中 x∈A, y∈B. .13: },104|{},31|{)5(;32:,,(4);: },1|{},10|{)3(;32:,,)2(;3:,)1(21xyxfyyBxxAxxyxfRBRAxyxfyyBxxAxyxfZBNAxyxfNBA其中构成映射的是 . 例 3 ．(2)(4)(5)其中构成映射的是 . 下列对应关系(A 到 B)中,其中 x∈A, y∈B. 例 3 ．.13: },104|{},31|{)5(;32:,,(4);: },1|{},10|{)3(;32:,,)2(;3:,)1(21xyxfyyBxxAxxyxfRBRAxyxfyyBxxAxyxfZBNAxyxfNBA(1) 集合 A ＝ {P|P 是数轴上的点 } ，集合 B ＝ R ， 对应关系 f...