正弦函数余弦函数的图象1VIP免费

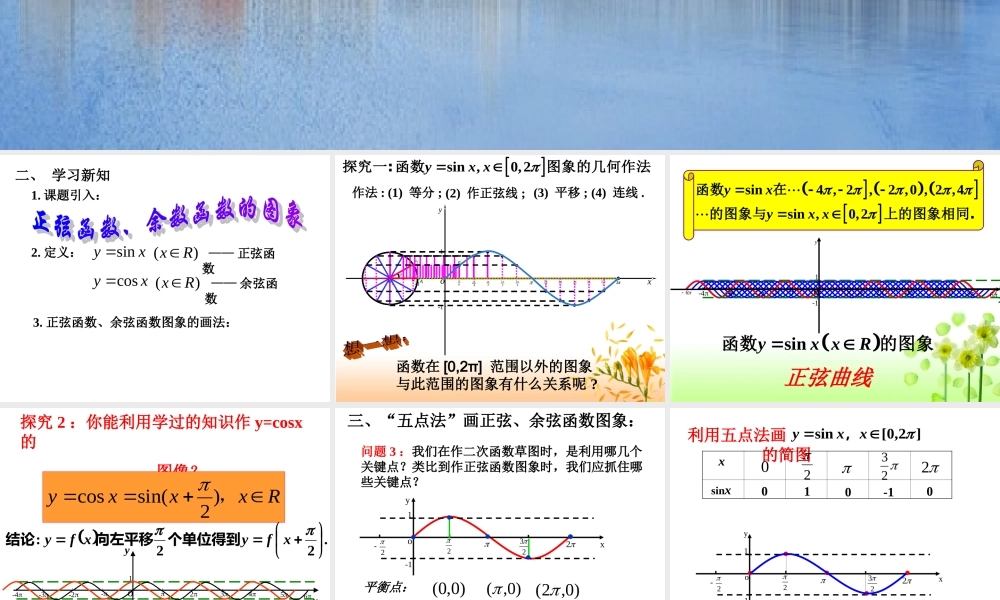
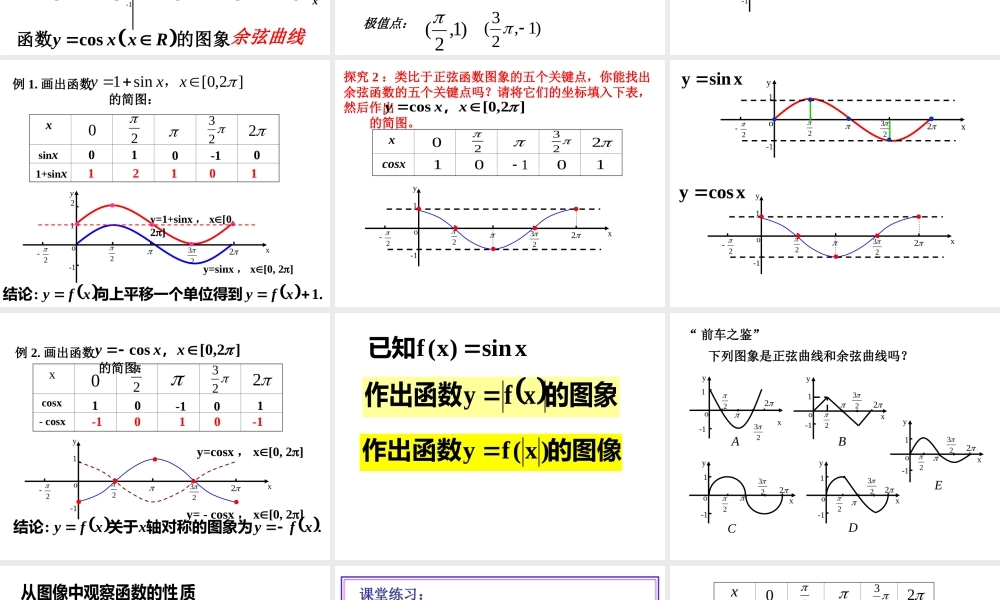
正弦函数、余弦函数的图象 1. 课题引入：二、 学习新知 2. 定义：xysinxycos —— 正弦函数 —— 余弦函数3. 正弦函数、余弦函数图象的画法：)(Rx)(Rx 2sin ,0,2yx x探究一:函数图象的几何作法oxy---11---1--1oA作法 : (1) 等分 ;3232656734233561126(2) 作正弦线 ; (3) 平移 ;61P1M/1p(4) 连线 .函数在 [0,2π] 范围以外的图象与此范围的图象有什么关系呢 ? 正弦曲线2o46246xy---------1-1  sin4 , 2,2 ,0 , 2 ,4sin ,0,2yxyx x函数在的图象与上的图象相同.sinyx xR函数的图象x6o--12345-2-3-41 探究 2 ：你能利用学过的知识作 y=cosx的 图像？x6yo--12345-2-3-41Rxxxy，)2sin(cos余弦曲线cosyx xR函数的图象 .22:xfyxfy个单位得到向左平移结论 三、“五点法”画正弦、余弦函数图象：问题 3 ：我们在作二次函数草图时，是利用哪几个关键点？类比到作正弦函数图象时，我们应抓住哪些关键点？平衡点：极值点：)0,0()0,()0,2( )1,2()1,23(1-1yxo22322 yxo1-122322利用五点法画 的简图]2,0[sinxxy， x sinx010-1002223 例 1. 画出函数 的简图：]2,0[sin1xxy， x sinx 1+sinx010-10 1 2 1 0 1 o1yx22322-12y=sinx ， x[0, 2]y=1+sinx ， x[0, 2]02223  .1:xfyxfy向上平移一个单位得到结论 探究 2 ：类比于正弦函数图象的五个关键点，你能找出余弦函数的五个关键点吗？请将它们的坐标填入下表，然后作出 的简图。]2,0[cosxxy，yxo1-122322 x cosx2230200111 1-1yxo22322yxo1-122322xsiny xcosy  yxo1-122322 x cosx - cosx10-101 -1 0 1 0 -1 y= - cosx ， x[0, 2]y=cosx ， x[0, 2]]2,0[cosxxy，例 2. 画出函数 的简图：02223  .:xfyxxfy轴对称的图象为关于结论  的图象作出函数xfy xsin)x(f已知的图像作出函数)x(fy  “ 前车之鉴”下列图象是正弦曲线和余弦曲线吗？yxo1-1223...