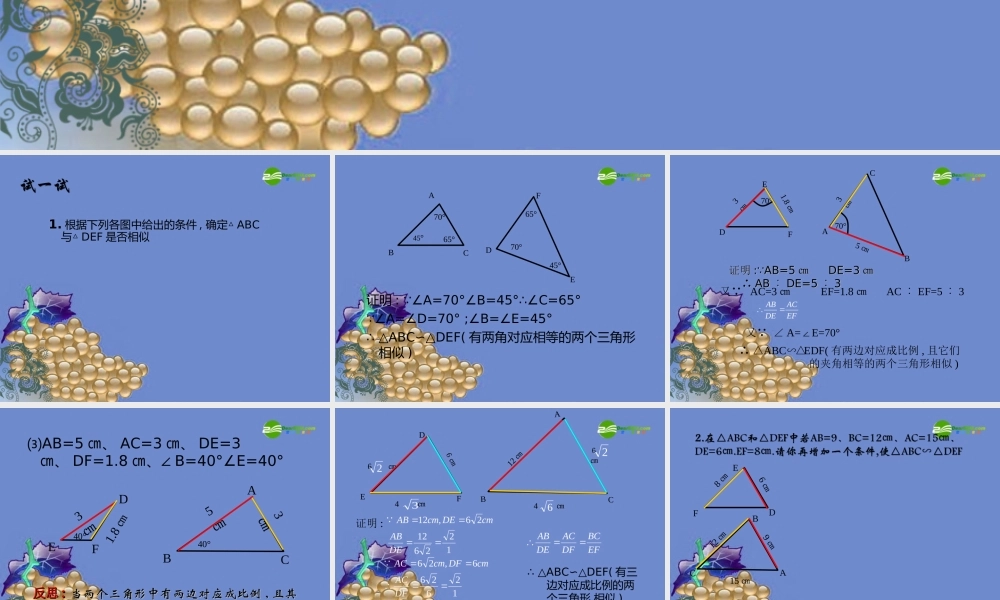
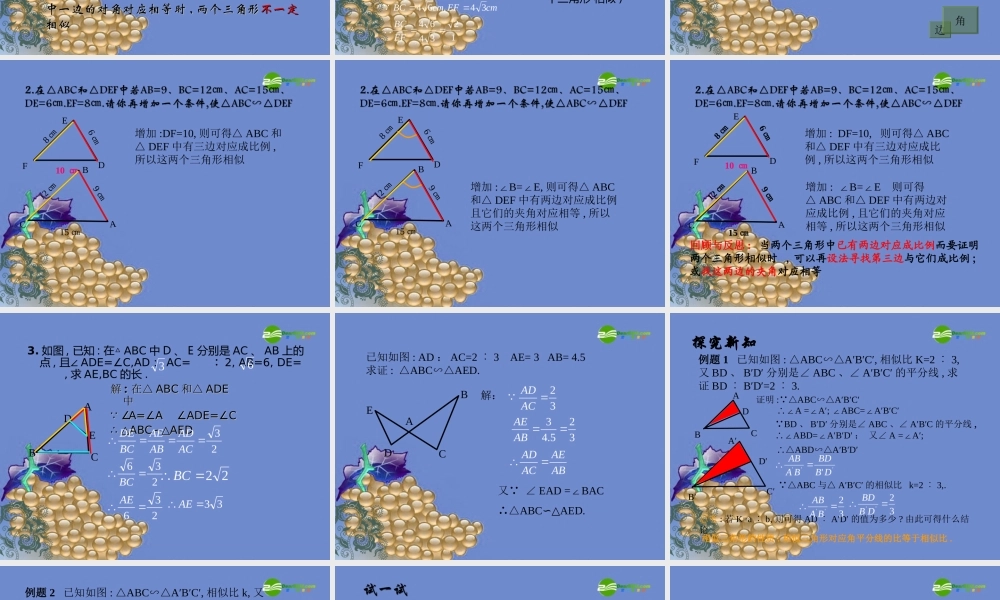
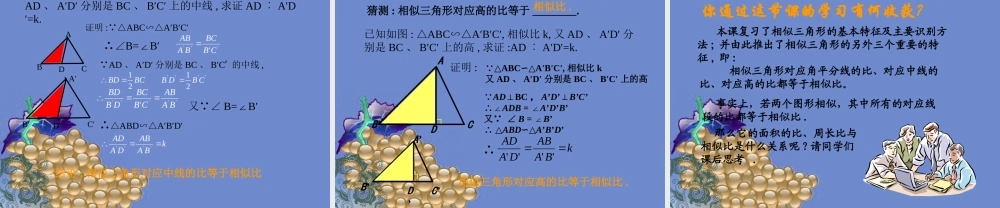
24.3 相似三角形的性质1. 根据下列各图中给出的条件 , 确定△ ABC与△ DEF 是否相似证明 : ∠A=70°∠B=45°∴∠C=65° ∠A=∠D=70° ;∠B=∠E=45° ∴ △ABC∽△DEF( 有两角对应相等的两个三角形相似 )ABC45°70°65°DFE65°70°45°证明证明 : AB=5: AB=5 ㎝ ㎝ DE=3DE=3 ㎝ ㎝ ∴∴ ABAB ︰︰ DE=5DE=5 ︰︰ 33 EDF70°3㎝1.8 ㎝ACB5 ㎝3㎝70°又 AC=3 ㎝ EF=1.8 ㎝ AC ︰ EF=5 ︰ 3又 ∠ A=E=70°∠ ∴ △ABCEDF(∽△有两边对应成比例 , 且它们 的夹角相等的两个三角形相似 )⑶AB=5 ㎝、 AC=3 ㎝、 DE=3㎝、 DF=1.8 ㎝、∠ B=40°∠E=40°BCAFDE40°1.8 ㎝40°5㎝3㎝3㎝反思反思 :: 当两个三角形中有两边对应成比例当两个三角形中有两边对应成比例 ,, 且其且其中一边的对角对应相等时中一边的对角对应相等时 ,, 两个三角形两个三角形不一定不一定相似相似∴ △ABC∽△DEF( 有三边对应成比例的两个三角形 相似 )DEF6㎝ACB12 ㎝6 ㎝4 ㎝6 ㎝4 ㎝证明 :边角EFD6 ㎝BAC12 ㎝9 ㎝15 ㎝8 ㎝BAC12 ㎝9 ㎝15 ㎝EFD6 ㎝8 ㎝10 ㎝增加 :DF=10, 则可得△ ABC 和△ DEF 中有三边对应成比例 ,所以这两个三角形相似BAC12 ㎝9 ㎝15 ㎝EFD6 ㎝增加 :B=E,∠∠则可得△ ABC和△ DEF 中有两边对应成比例且它们的夹角对应相等 , 所以这两个三角形相似8 ㎝BAC12 ㎝9 ㎝15 ㎝EFD6 ㎝8 ㎝10 ㎝增加 : DF=10, 则可得△ ABC和△ DEF 中有三边对应成比例 , 所以这两个三角形相似增加 : B=E ∠∠则可得△ ABC 和△ DEF 中有两边对应成比例 , 且它们的夹角对应相等 , 所以这两个三角形相似回顾与反思 : 当两个三角形中已有两边对应成比例而要证明两个三角形相似时 , 可以再设法寻找第三边与它们成比例 ;或找这两边的夹角对应相等 3. 如图 , 已知 : 在△ ABC 中 D 、 E 分别是 AC 、 AB 上的点 , 且∠ ADE=∠C,AD : AC= ︰ 2, AB=6, DE= , 求 AE,BC 的长 .解解 :: 在△在△ ABCABC 和△和△ ADEADE中中 ∠∠A=∠A ∠ADE=∠CA=∠A ∠ADE=∠C∴ △∴ △ABC∽△AED ABC∽△AED ADBCE已知如图 : AD : AC=2 ︰ 3 AE= 3 AB= 4.5 求证 : ABCAED.△∽△AEDCB又 ∠ EAD =BAC∠∴△ABCAED.∽△解:探究新知 例题 1 已知如图 : ABCA′B′C′,△∽△相似比 ...