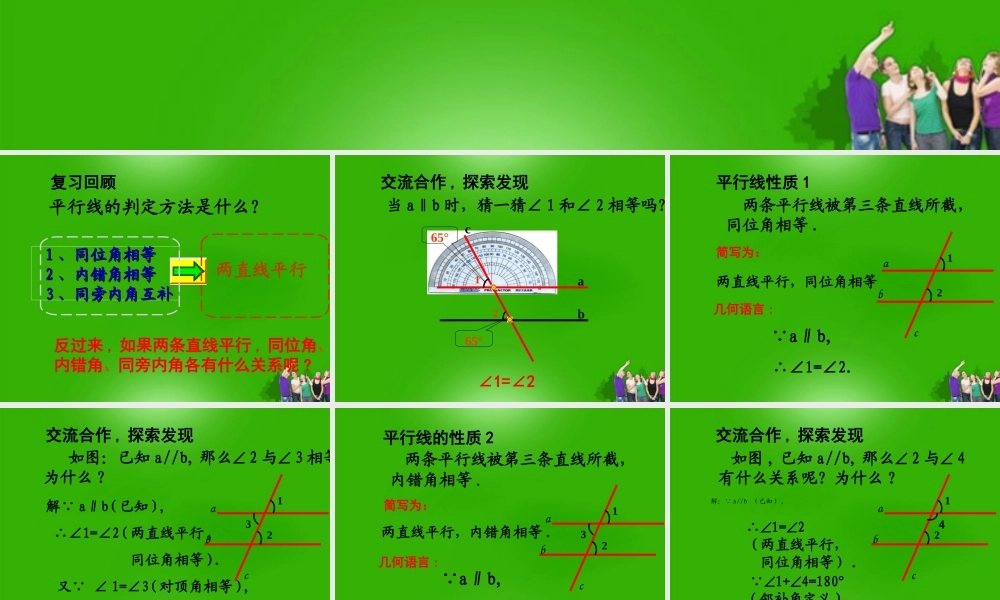
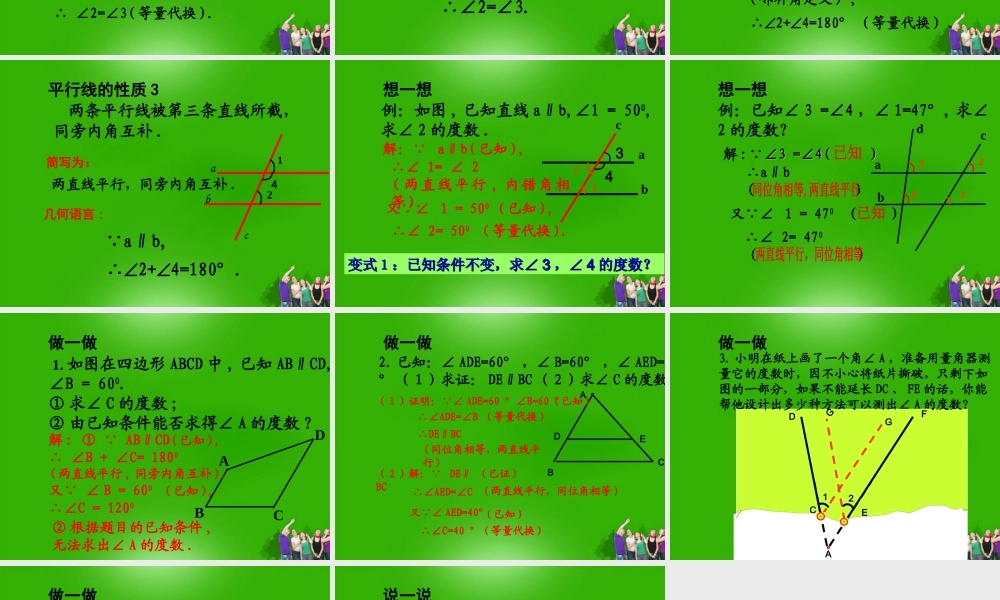
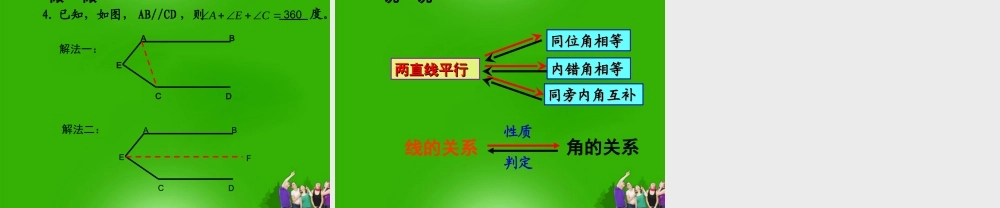
第四章 图形的初步认识复习回顾两直线平行 11 、同位角相等、同位角相等22 、内错角相等、内错角相等 33 、同旁内角互补、同旁内角互补平行线的判定方法是什么?反过来 , 如果两条直线平行 , 同位角、内错角、同旁内角各有什么关系呢 ?交流合作 , 探索发现当 a‖b 时,猜一猜∠ 1 和∠ 2 相等吗?ab1265°65°c∠1=∠2两直线平行,同位角相等 两条平行线被第三条直线所截, 同位角相等 .∴∠1=∠2. a∥b,简写为:几何语言 :b12ac平行线性质 1 如图:已知 a//b, 那么 2 与 3 相等吗?为什么 ?解 a∥b( 已知 ), ∴∠1=∠2( 两直线平行 , 同位角相等 ). 又 ∠ 1=∠3( 对顶角相等 ), ∴ ∠2=∠3( 等量代换 ).b12ac3交流合作 , 探索发现两直线平行,内错角相等 .平行线的性质 2 两条平行线被第三条直线所截, 内错角相等 .∴∠2=∠3. a∥b,简写为:b12ac3几何语言 :解: a//b (已知) , 如图 , 已知 a//b, 那么 2 与 4有什么关系呢?为什么 ?b12ac4∴1=2(两直线平行, 同位角相等) . 1+4=180°(邻补角定义) ,∴2+4=180° (等量代换) .交流合作 , 探索发现两直线平行,同旁内角互补 . 两条平行线被第三条直线所截, 同旁内角互补 .∴2+4=180°. a∥b,简写为:b12ac4平行线的性质 3几何语言 :例:如图 , 已知直线 a∥b,∠1 = 500,求∠ 2 的度数 .abc12∴∠ 2= 500 ( 等量代换 ).解: a∥b( 已知 ),∴∠ 1= ∠ 2( 两直 线平行 , 内错角相等 ).又 ∠ 1 = 500 ( 已知 ),变式1:已知条件不变,求∠变式1:已知条件不变,求∠ 33 ,∠,∠ 44 的度数?的度数? 34想一想例:已知∠ 3 =∠4 ,∠ 1=47°, 求∠2 的度数?∴∠ 2= 470( )解 : ∠3 =∠4(∠3 =∠4( ))∴a∥b( )又 ∠ 1 = 470 ( )c1234abd想一想 1. 如图在四边形 ABCD 中 , 已知 AB∥CD,∠B = 600.① 求∠ C 的度数 ;② 由已知条件能否求得∠ A 的度数 ?BACD解 : ① AB∥CD( 已知 ),∴ ∠B + ∠C= 1800( 两直线平行 , 同旁内角互补 ).又 ∠ B = 600 ( 已知 ),∴∠C = 1200② 根据题目的已知条件 ,无法求出∠ A 的度数 .做一做EDCBA(已知)( 1 )证明: ∠ ADE=60 °∠B=60 °∴∠ADE=∠B (等量代换)∴DE∥BC( 同位角相等,两直线平行...