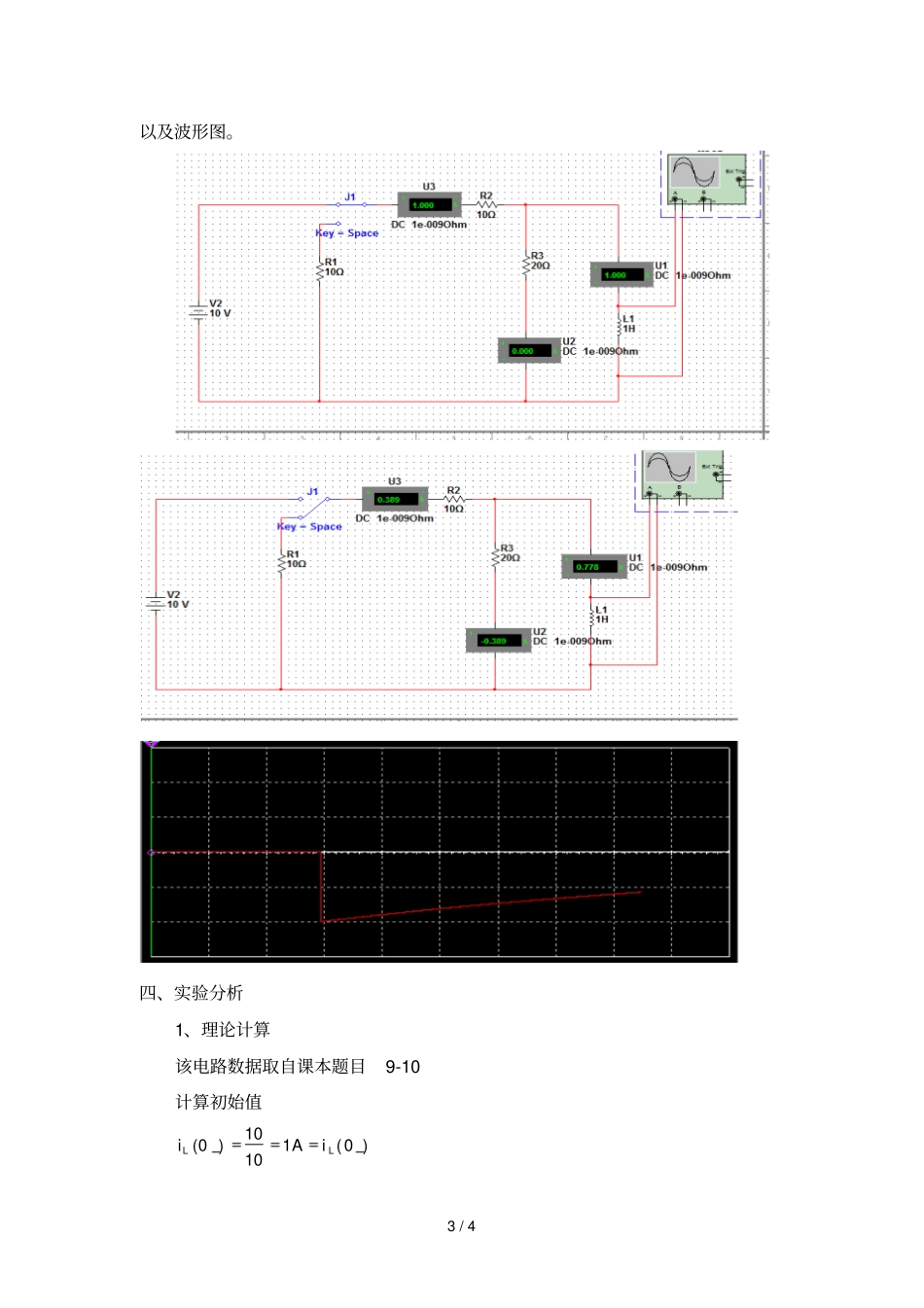
1 / 4 实验一直流激励下的 RL 一阶电路的响应一、实验目的1、了解一阶电路的基本知识;2、通过仿真验证一阶电路的换路定理、三要素法;3、验证一阶电路的暂态过程中电压、电流的关系式。二、原理说明之前所学,都是在电路已经处于稳定状态的情况下,讨论激励和响应的关系,称为稳态分析。 当电路中含有储能元件, 即含有电感和电容元件, 这类元件的电压和电流关系式微分、 积分关系而不是代数关系, 因此根据基尔霍夫定理和元件特性方程所列写的电路方程, 是以电路或电压为变量的微分方程。故称这类元件为动态元件, 含有动态元件的电路称为动态电路。如果只含有一个动态元件, 描述电路的特性方程是一阶微分方程,这种电路称为一阶电路。在动态电路中,当电路的结构或元件的参数发生改变时(例如,电路中电源或无源元件的断开或接入,信号的突然注入等),可能使电路改变原来的工作状态,而转变到另一个工作状态, 这种转变往往需要经历一个过程,工程上称为过渡过程。过渡过程又称为过渡状态或暂态。在描述电路过渡过程的微分方程中, 电路的任何电压和电流及其n-1 阶导数在 t=0+ 时的值称为初始值。其中电感电流和电容电压的初始值,即)0(Li和)0(cu称为独立的初始值, 其余的称为非独立的初始值。 独立的初始值决定了电路的初始能量。在电路前后电容电流和电感电压为有限值的条件下,换路前后瞬间电容电压cu 和电感电流ci 不能跃变。即)0()0(LLii)0()0(ccuu上述两个式子,称为换路定理。一阶电路可以分为零状态响应、零输入响应和全响应三种情况,其中零状态响应和零输入响应为全响应的特殊情况。2 / 4 实际计算过程, 可以运用一阶电路的等效化简和三要素法,讨论电路中的电压电流情况。但三要素法只适用于在直流或正弦信号激励时的一阶电路。三要素法运用步骤和方法包括一下4 步:1)计算电压或电流的初始值)0(f。对于电容电压和电感电流可以通过换路定理求的。而除此之外的初始值,可根据0 等效电路求的。在等效电路中,电感相当于)0(LiI的电流源,电容相当于)0(cuU的电压源。2)计算电压或电流的稳态值)(f。把换路后电路中的所有电容看成开路,所有电感当作短路处理。3)计算电路的时间常数 τ 。对于 τ 中的电阻应该理解为是从L 或 C 元件两端向电路的其余部分看进去的入端电阻。4)将以上求得的三要素代入下式,即得所求响应的全响应表达式。teffftf)]()0([)()(dtdiLuLLdtduCicc三、实验内容 1 ...