正切函数的性质与图象VIP免费

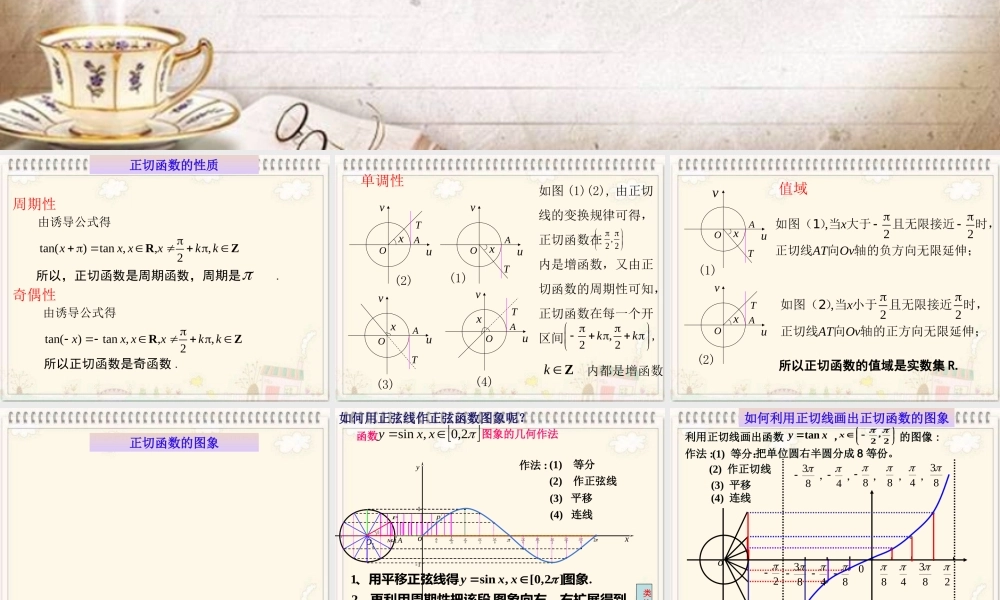
§ 周期性tan()tan ,,,2xx xxkk   RZ由诱导公式得所以，正切函数是周期函数，周期是 .奇偶性tan()tan ,,,2xx xxkk RZ由诱导公式得所以正切函数是奇函数 .正切函数的性质 单调性xuvTAOxuvTAOuxuvTAOxvTAO(1)(2)(4)(3)如图 (1)(2), 由正切线的变换规律可得，正切函数在 内是增函数，又由正切函数的周期性可知，正切函数在每一个开区间 内都是增函数 .,2 2 ,,22kk  k Z 值域xuTAO(1),22xATOv如图（1）当 大于且无限接近时，正切线向轴的负方向无限延伸；xuvTAO(2),22xATOv如图（2）当 小于且无限接近时，正切线向轴的正方向无限延伸；v所以正切函数的值域是实数集 R. 正切函数的图象 2 函数2,0,sinxxy图象的几何作法oxy---11---1--1oA作法 : (1) 等分3232656734233561126(2) 作正弦线(3) 平移61P1M/1p(4) 连线如何用正弦线作正弦函数图象呢？用正切线作正切函数 y=tanx 的图象.]2,0[,sin1图象、用平移正弦线得xxy 类 比.2图象向左、右扩展得到、再利用周期性把该段 作法 :(1) 等分：(2) 作正切线(3) 平移(4) 连线把单位圆右半圆分成 8 等份。83488483，，，，，利用正切线画出函数 ， 的图像 : xytan 22 ，x44288838320o如何利用正切线画出正切函数的图象 叫做正切曲线 .0223223tan ,()2yx xxkk RZ利用正切函数的周期性，把图象向左、右扩展，得到正切函数且的图象，并把它,,2xkk Z.从图中可以看出 正切曲线是由被相互平行的直线所隔开的无穷多支曲线组成的渐进线渐进线正切函数的图象xy ⑴ 定义域：}Zk,k2x|x{⑵ 值域：⑶ 周期性：⑷ 奇偶性： 正切函数的性质奇函数，图象关于原点对称。R⑸ 单调性：Zk,2kx(6) 渐近线方程： 渐近线渐近线 在每一个开区间 ， 内都是增函数。)2,2(kkZk (1) 正切函数是整个定义域整个定义域上的增函数吗？为什么？(2) 正切函数会不会在某一区间内是减函数？为什么？ 问题：AB 在每一个开区间 ， 内都是增函数。ππ(-+ kπ, + kπ)22kZ问 题 讨 论 关于正切函数 , 下列判断不正确的是（ ）tanyxA 是奇函数B 在整...