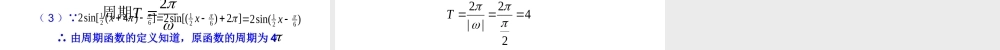正弦余弦函数的性质VIP免费

1.4.2 正弦函数、余弦函数的性质观察图像，找出图像的共同点：（ 1 ）定义域： R（ 2 ）值域： [-1 ， 1]（ 3 ）图象有规律地不断重复出现。正弦函数的图象探究余弦函数的图象x22322523yO23225311x22322523yO23225311| sin|1| cos|1≤≤xx（ 1 ）图象特征：图象从Ｘ轴看等距离重复出现；（ 2 ）数值特征：当自变量 x 每增加 的整数倍时，函数值重复出现。（ 3 ）定义：若存在一个非零常数 T ，使得当 x 取定义域内的每一个值时，都有 f(x+T)=f(x) 成立，则称函数 f(x) 为周期函数；非零常数 T 叫做这个函数的周期．（ 4 ）最小正周期：如果在周期函数的所有周期中存在一个最小的正数，则称这个最小的正数为函数的最小正周期。2一、周期性正弦函数的图象x22322523yO23225311正弦函数的和余弦函数的的最小正周期为23 、周期函数不一定存在最小正周期。例如 f(x)=c2 、非唯一性——周期函数的周期不止一个，例如， 都是正弦函数的周期。2 ,4 ,6 ,2 , 4 , 6和1 、存在性——要求对于定义域中的每一个值 x, 均有 f(x+T)=f(x) 。注意1 1 y 3cos x,xR(2)y=sin 2x,xRx(3)y2sin(),xR26例求下列函数的周期( ) =.,都指最小正周期若不加特别说明解：（ 1 ）∵3cos(2 )3cosxx∴ 由周期函数的定义知道，原函数的周期为 2（ 2 ）∵ sin 2()x∴ 由周期函数的定义知道，原函数的周期为sin(22 )x sin 2x（ 3 ）∵ 1262sin[ (4 )]x∴ 由周期函数的定义知道，原函数的周期为 41262sin[()2 ]x1262sin()x2TT4T思考：函数的周期与解析式中的哪些量有关？)cos()sin(xAyxAy与函数函数2T周期例题例题(1) ( )sin(2)5f xx1(2) ( )cos()232xf x求下列函数的周期练习：1222T422||2T