指数函数 (3)VIP免费

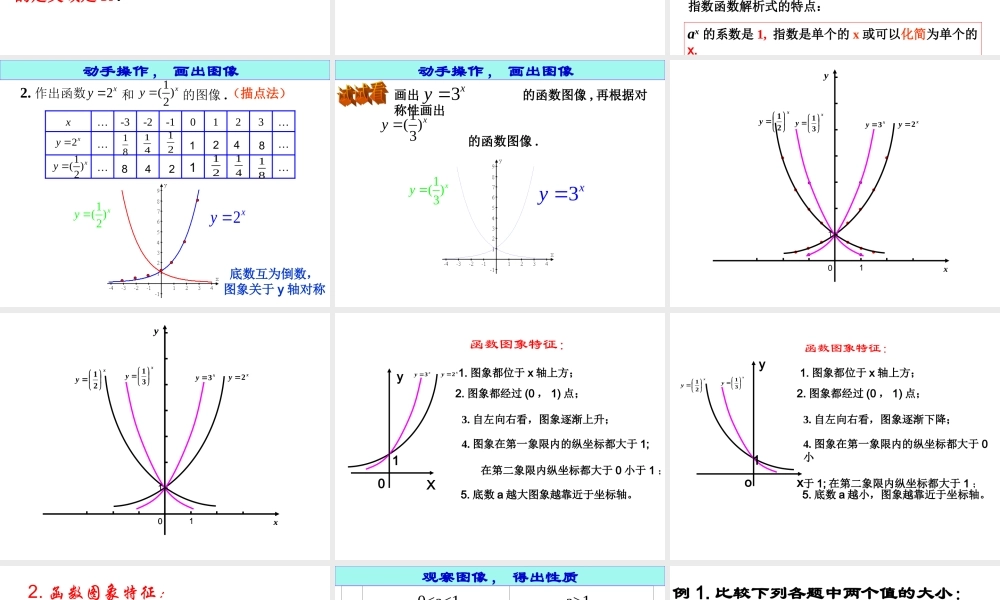
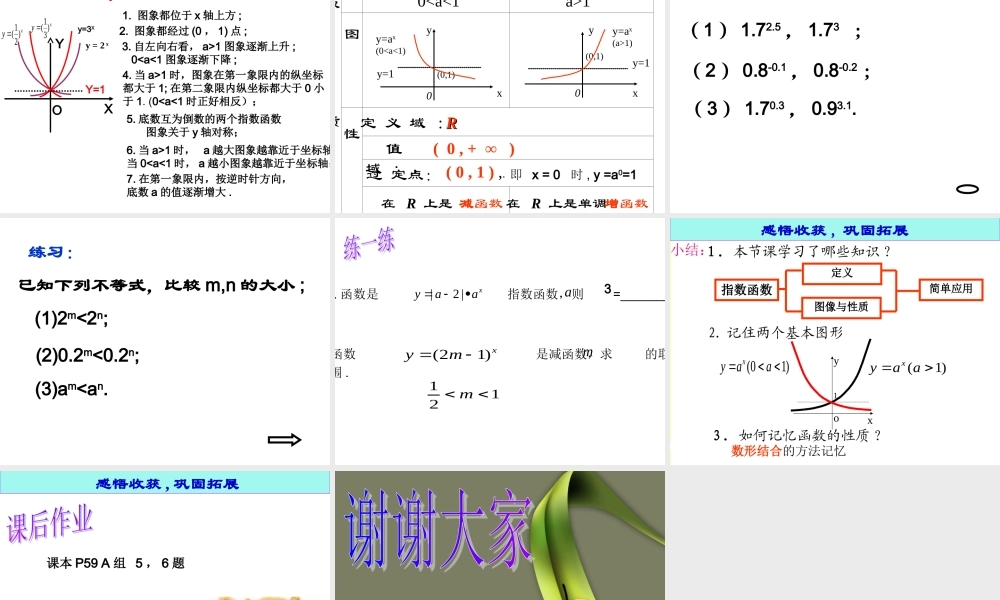
复习提问：1. 正分数指数幂的意义。2. 有理数指数幂的运算性质。 引例 1 一张白纸对折一次得 2 层，对折两次得 4 层，对折 3 次得 8 层，若对折 x 次所得层数为ｙ，则 y 与 x 的函数关系是：Y=2x创设情景 引例 2 一尺之棰 , 日取其半 , 万世不竭 . 创设情景 出自《庄子● 天下篇》 设木杖 原长为１个单位截取次数１２３…剩余长度…214181剩余长度 y 关于截取次数 x 的表达式为 :…1( )2xy 1( )2xx引入概念从两个实例中抽象出两个函数解析式1. 指数函数的定义：12( )2xxyy与这两个解析这两个解析式有何共同式有何共同特点特点 ??这两个解析这两个解析式有何共同式有何共同特点特点 ?? 一般地，函数 y = ax (a0 ，且 a 1) 叫做指数函数，其中 x 是自变量 . 函数的定义域是 R .y 与 x 之间是函数 关系吗？xya概念剖析为何规定 a0 ，且 a1?而当 a=1 时，函数值 y 恒等于 1 ，没有研究的必要 .xya当 a0 时， ax 有些会没有意义，如（ -2 ）， 00 等都没有意义；12 概念剖析下列哪些是指数函数？ax 的系数是 1, 指数是单个的 x 或可以化简为单个的x.1( )2x8x2(1)yx(2)2xy (3)2 xy(4)2 3xy  3(5)2 xy 1(6)3xy指数函数解析式的特点： 2. 作出函数和的图像 . 2xy 1( )2xy 1( )2xy 2xy 动手操作 , 画出图像 （描点法）底数互为倒数，图象关于 y 轴对称……………3210-1-2-3…x2xy 1( )2xy 21418121418181248421 动手操作 , 画出图像 画出 的函数图像 , 再根据对称性画出 的函数图像 .1( )3xy 3xy 3xy 1( )3xy  xy2xy 21xy3xy 31011xy 011xyxy 21xy 31xy2xy3011xy 函数图象特征：xy2xy3X10y1. 图象都位于 x 轴上方；2. 图象都经过 (0 ， 1) 点；3. 自左向右看，图象逐渐上升；4. 图象在第一象限内的纵坐标都大于 1; 在第二象限内纵坐标都大于 0 小于 1 ； 5. 底数 a 越大图象越靠近于坐标轴。 xy 21xy 31xyo11. 图象都位于 x 轴上方；2. 图象都经过 (0 ， 1) 点；3. 自左向右看，图象逐渐下降；5. 底数 a 越小，图象越靠近于坐标轴。4. 图象在第一象限内的纵坐标都大于 0小于 1; 在第二象限内纵坐标都...