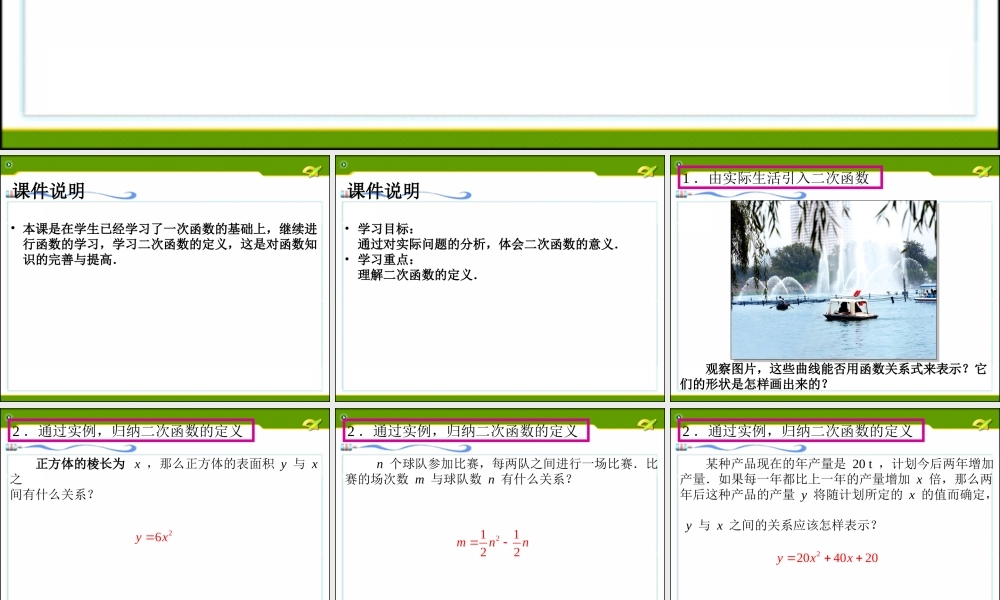
22.1 二次函数的图象和性质(第 1 课时)九年级 上册• 本课是在学生已经学习了一次函数的基础上,继续进行函数的学习,学习二次函数的定义,这是对函数知识的完善与提高.课件说明• 学习目标:通过对实际问题的分析,体会二次函数的意义. • 学习重点:理解二次函数的定义. 课件说明 观察图片,这些曲线能否用函数关系式来表示?它们的形状是怎样画出来的?1 .由实际生活引入二次函数 正方体的棱长为 x ,那么正方体的表面积 y 与 x 之间有什么关系? 2 .通过实例,归纳二次函数的定义26yx n 个球队参加比赛,每两队之间进行一场比赛.比赛的场次数 m 与球队数 n 有什么关系?21122mnn2 .通过实例,归纳二次函数的定义 某种产品现在的年产量是 20 t ,计划今后两年增加 产量.如果每一年都比上一年的产量增加 x 倍,那么两 年后这种产品的产量 y 将随计划所定的 x 的值而确定, y 与 x 之间的关系应该怎样表示? 2204020yxx2 .通过实例,归纳二次函数的定义 这三个函数关系式有什么共同点? 26xy nnm21212 2040202xxy2 .通过实例,归纳二次函数的定义 二次函数的定义:一般地,形如 ( a , b , c 是常数, a≠0 ) 的函数,叫做二次函数.其中, x 是自变量, a ,b , c 分别是函数解析式的二次项系数、一次项系数和常数项.cbxaxy22 .通过实例,归纳二次函数的定义 例某小区要修建一块矩形绿地,设矩形的长为 x m ,宽为 y m ,面积为 S m 2 ( x > y ). ( 1 )如果用 18 m 的建筑材料来修建绿地的边缘(即周长),求 S 与 x 的函数关系,并求出 x 的取值范围. ( 2 )根据小区的规划要求, 所修建的绿地面积必 须是 18 m 2 ,在满足( 1 )的条件下,矩形的长和宽各为多少 m ?3 .练习、巩固二次函数的定义3 .练习、巩固二次函数的定义解:( 1 )由题意,得 . x > y > 0 , ∴ x 的取值范围是< x < 9 , ∴29xyyx91822,S 矩形 = xy = x 9 - x = -x2+9x .( ) ( 2 ) 当矩形面积 S 矩形 = 18 时,即 - x 2 + 9x = 18 , 解得 x1 = 3 , x2 = 6 . 当 x = 3 时, y = 9 - 3 = 6 ,但 y > x ,不合题意,舍去. 当 x = 6 时, y = 9 - 6 = 3 . 所以当绿地面...