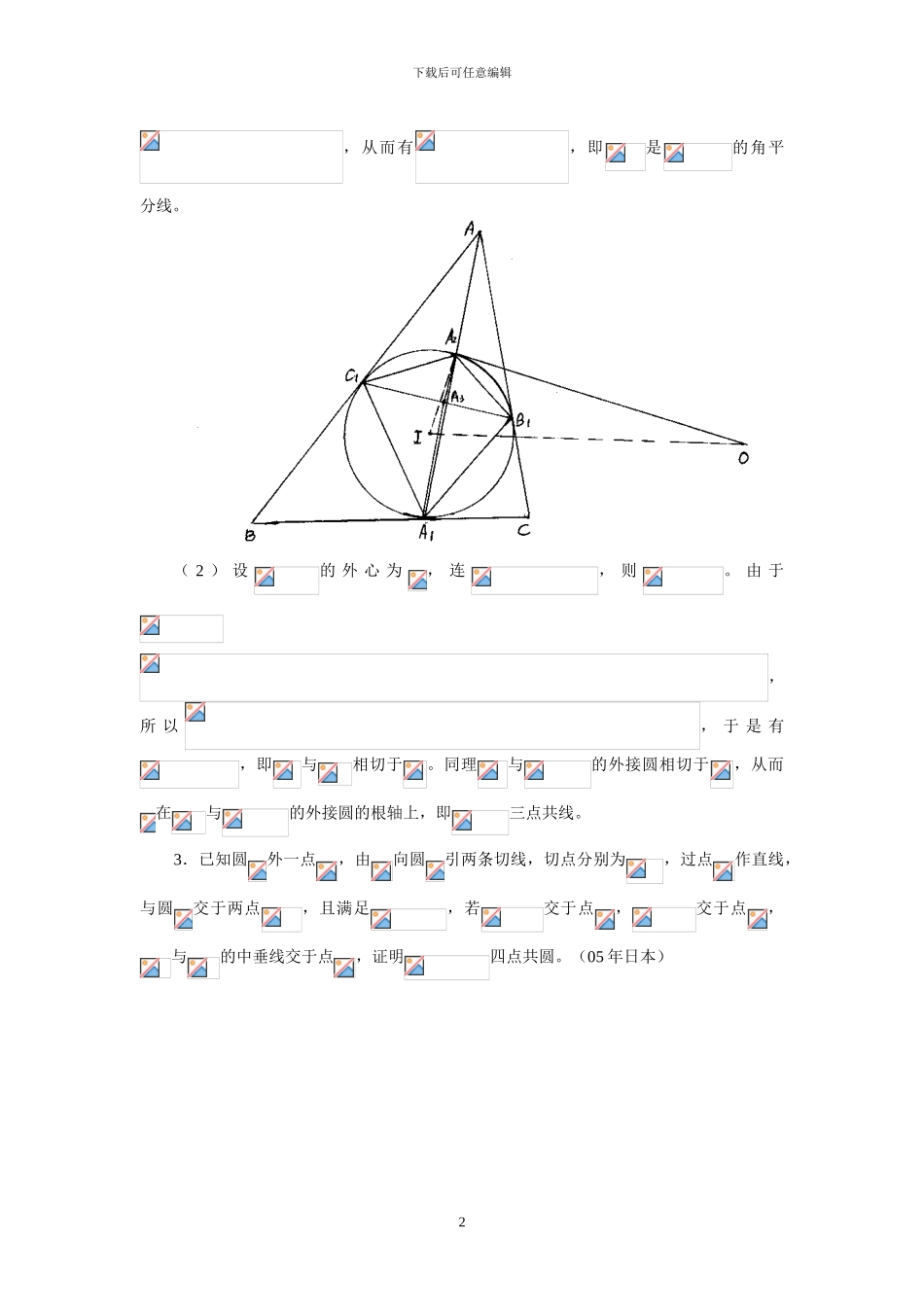
下载后可任意编辑2024 年国家集训队平面几何讲义1.一圆切于两条平行线,第二个圆切于,外切于,第三个圆切于,外切于,外切于,交于,求证是的外心。(35 届 IMO 预选题)证明 由∥,知,从而有,即三 点 共 线 。 同 理 由∥, 可 得三 点 共 线 。 又 因 为, 所 以四 点 共 圆 ,,即点在与的根轴上。又因为在与的根轴上,所以是与的根轴。同理是与的根轴,因此为根心,且有,即是的外心。2.非等腰的内切圆圆心为,其与分别相切于点,分别交圆于, 中的角平分线分别交于点,证明(1)是的角平分线;(2)假如是和的两个外接圆的交点,则点在直线上。(01 年保加利亚)证 明 ( 1 ) 因 为∽,∽, 所 以 有1下载后可任意编辑,从而有,即是的角平分线。( 2 ) 设的 外 心 为, 连, 则。 由 于,所 以, 于 是 有,即与相切于。同理与的外接圆相切于,从而在与的外接圆的根轴上,即三点共线。3.已知圆外一点,由向圆引两条切线,切点分别为,过点作直线,与圆交于两点,且满足,若交于点,交于点,与的中垂线交于点,证明四点共圆。(05 年日本)2下载后可任意编辑证明 因为是调和点列,且,所以在关于点的阿波罗尼斯圆上。连,有。设的外接圆与交于点,则有,即在的中垂线上,从而有,因此四点共圆。4.若到的三个顶点的距离的比都是,且互不相等,则直线过的外接圆的一条直径。若设的外接圆圆心为,则。证明 法一:由于到的距离之比为,则在阿波罗尼斯圆上,其中与的交点为,且为调和点列。设与交于点,则,因此与相切于点,于是也与相切于点。3下载后可任意编辑同理,由于到的距离之比为,则在阿波罗尼斯圆上,设与交于点,于是与相切于点。因为,所以在与的 根 轴 上 , 从 而 有三 点 共 线 。 设与交 于 点, 则,即为调和点列。法二 由于,则的外接圆就是关于点的阿波罗尼斯圆,从而在直线上,且有。5.已知圆心分别为的圆外切于点,并内切于圆,切点分别为,过点作的公切线 。设圆的直径垂直于 ,使得在 的同侧,证明三线交于一点。(第 47 届 IMO 预选题)证明 设的中点为,为圆与圆的位似中心,由于半径分别垂直于 ,所以∥,且有三点共线。同理三点共线。设交于点,由于,所以是的垂心,于是,这表明在直线 上。设与直线 交于点,下面证明点在直线上。设与圆的第二个交点为,则是圆的直径,由梅涅劳斯定理的逆定理,要证三点共线,只要证4下...