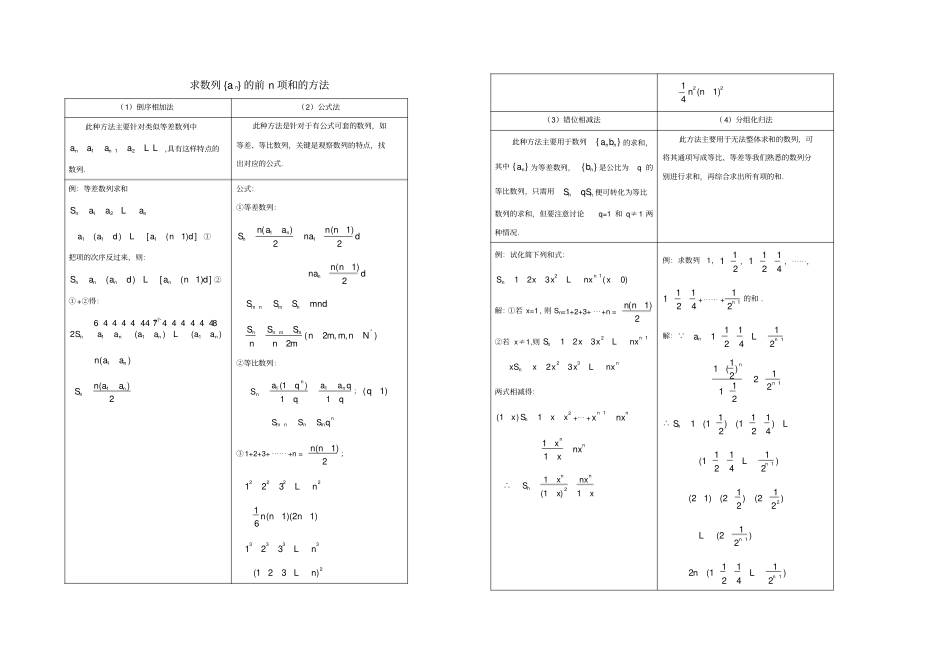
求数列 {a n} 的前 n 项和的方法( 1)倒序相加法(2)公式法此种方法主要针对类似等差数列中112nnaaaaL L,具有这样特点的数列.此种方法是针对于有公式可套的数列,如等差、等比数列,关键是观察数列的特点,找出对应的公式.例:等差数列求和12nnSaaaL111()[(1) ]aadandL①把项的次序反过来,则:()[(1) ]nnnnSaadandL②①+②得:1112()()nnnnnSaaaaaa6 4 4 4 4 44 7 4 4 4 4 4 48L个1()nn aa1()2nnn aaS公式:①等差数列:11()(1)22nnn aan nSnad(1)2nn nnadm nmnSSSmnd*(2 ,,)2nn mmSSSnm m nNnnm②等比数列:qqaaqqaSnnn11)1(11; (1)qnm nnmSSS q③1+2+3+ ⋯⋯ +n = (1)2n n;2222123nL1(1)(21)6n nn3333123nL2(1 23)nL221(1)4n n(3)错位相减法( 4)分组化归法此种方法主要用于数列}{nnba的求和,其中}{na为等差数列,}{nb是公比为q 的等比数列,只需用nnSqS 便可转化为等比数列的求和,但要注意讨论q=1 和 q≠1 两种情况.此方法主要用于无法整体求和的数列,可将其通项写成等比、等差等我们熟悉的数列分别进行求和,再综合求出所有项的和.例:试化简下列和式:21123(0)nnSxxnxxL解:①若 x=1 ,则 Sn=1+2+3+ ⋯+n = (1)2n n②若 x≠1,则21123nnSxxnxL2323nnxSxxxnxL两式相减得:2(1)1nx Sxx +⋯ +nnnxx111nnxnxx∴21(1)1nnnxnxSxx例:求数列1,112,11124,⋯⋯,11124+⋯⋯ +112n的和 . 解: 11111242nnaL111( )1221212nn∴1111(1)(1)224nSL1111(1)242nL211(21)(2)(2)2211(2)2nL11112(1)242nnL11222nn( 5)奇偶求和法(6)裂项相消法此种方法是针对于奇、偶数项,要考虑符号的数列, 要求 Sn,就必须分奇偶来讨论,最后进行综合.此方法主要针对12231111nna aa aaaL这样的求和,其中{a n} 是等差数列.例:求和11357( 1)(21)nnSnL解:当 n = 2k (kN+) 时, 2(1 3)(57)nkSS[(43)(41)]kkL2kn当21()nkkN时 ,21222[ (41)]nkkkSSSakk21kn综合得:1( 1)nnSn例: {a n} 为首项为 a1,公差为 d 的等差数列,求12233411111nnnSa aa aa aaaL解: 1111()()kkkkkkkkadaa aaadd aadg1111111()()kkkkd aaddaa∴1223111111()()nSd aadaa1111()nndaaL122311111111[()()()]nndaaaaaaL1111()ndaa111[(1) ]na and(7) 分类讨论( 8)归纳—猜想—证明此方法是针对数列{na } 的其中几项符号与另外的项不同,而求各项绝对值的和的问题,主要是要分...