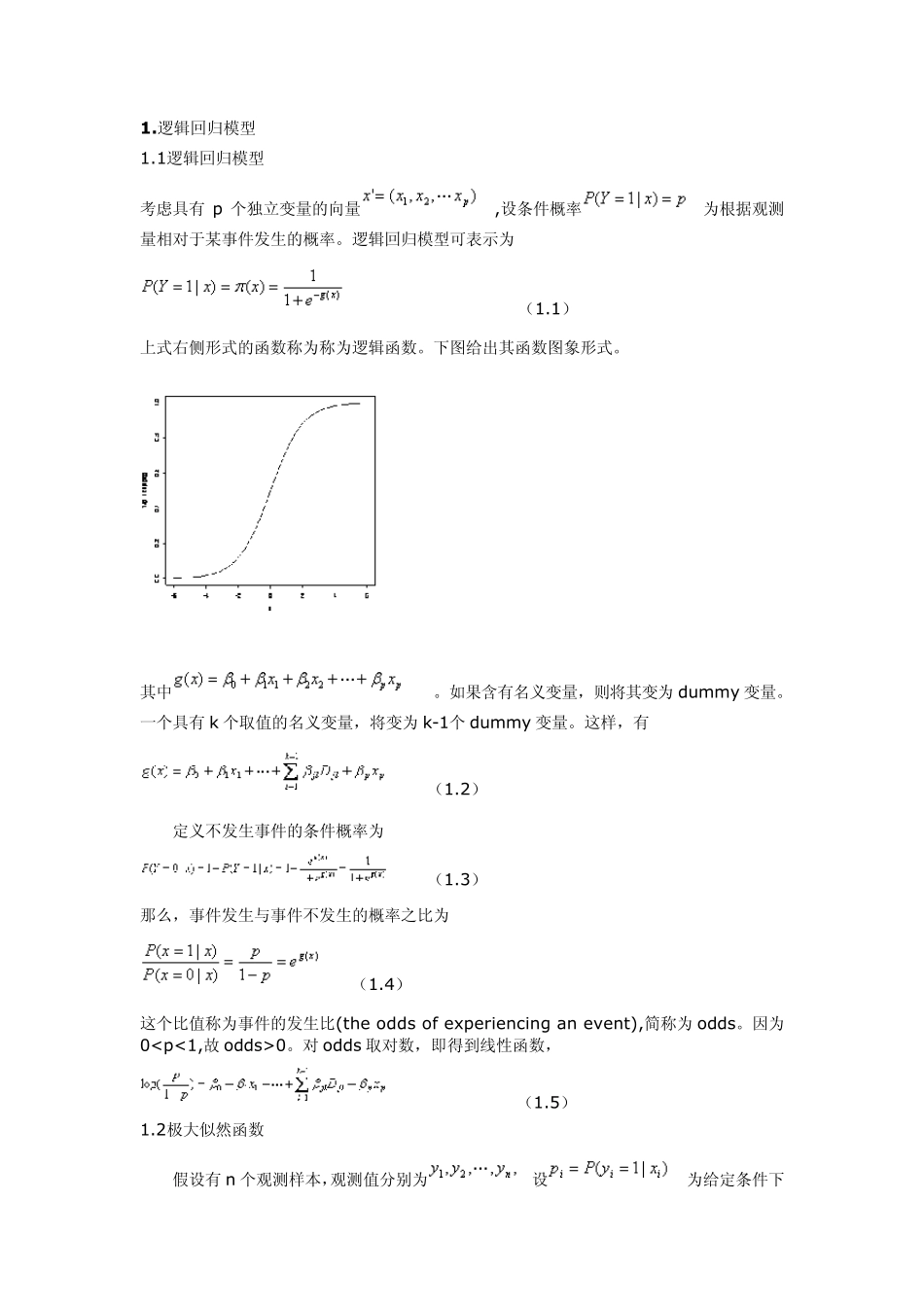
1 .逻辑回归模型 1.1逻辑回归模型 考虑具有p 个独立变量的向量,设条件概率为根据观测量相对于某事件发生的概率。逻辑回归模型可表示为 (1.1) 上式右侧形式的函数称为称为逻辑函数。下图给出其函数图象形式。 其中。如果含有名义变量,则将其变为dummy 变量。一个具有k 个取值的名义变量,将变为k-1个dummy 变量。这样,有 (1.2) 定义不发生事件的条件概率为 (1.3) 那么,事件发生与事件不发生的概率之比为 (1.4) 这个比值称为事件的发生比(the odds of experiencing an event),简称为odds。因为0
0。对odds 取对数,即得到线性函数, (1.5) 1.2极大似然函数 假设有n 个观测样本,观测值分别为设为给定条件下得到的概率。在同样条件下得到 的条件概率为。于是,得到一个观测值的概率为 (1.6) 因为各项观测独立,所以它们的联合分布可以表示为各边际分布的乘积。 (1.7) 上式称为 n 个观测的似然函数。我们的目标是能够求出使这一似然函数的值最大的参数估计。于是,最大似然估计的关键就是求出参数,使上式取得最大值。 对上述函数求对数 (1.8) 上式称为对数似然函数。为了估计能使取得最大的参数的值。 对此函数求导,得到p+1个似然方程。 (1.9) ,j=1,2,..,p. 上式称为似然方程。为了解上述非线性方程,应用牛顿-拉斐森(New ton-Raphson)方法进行迭代求解。 1.3 牛顿-拉斐森迭代法 对求二阶偏导数,即 Hessian 矩阵为 (1.10) 如果写成矩阵形式,以H表示 Hessian 矩阵,X表示 (1.11) 令 (1.12) 则。再令(注:前一个矩阵需转置),即似然方程的矩阵形式。 得牛顿迭代法的形式为 (1.13) 注意到上式中矩阵H为对称正定的,求解即为求解线性方程HX=U中的矩阵X。对H进行 cholesky 分解。 最大似然估计的渐近方差(asymptotic variance)和协方差(covariance)可以由信息矩阵(information matrix)的逆矩阵估计出来。而信息矩阵实际上是二阶导数的负值,表示为。估计值的方差和协方差表示为,也就是说,估计值的方差为矩阵I的逆矩阵的对角线上的值,而估计值和的协方差为除了对角线以外的值。然而在多数情况,我们将使用估计值的标准方差,表示为 ,for j=0,1,2,…,p (1.14) 2.显著性检验 下面讨论在逻辑回归模型中自变量是否与反应变量显著相关的显著性检验。零假设:=0(表示自变量对事件发生可能性无影响作用)。如果零假设...