线面所成的角VIP免费

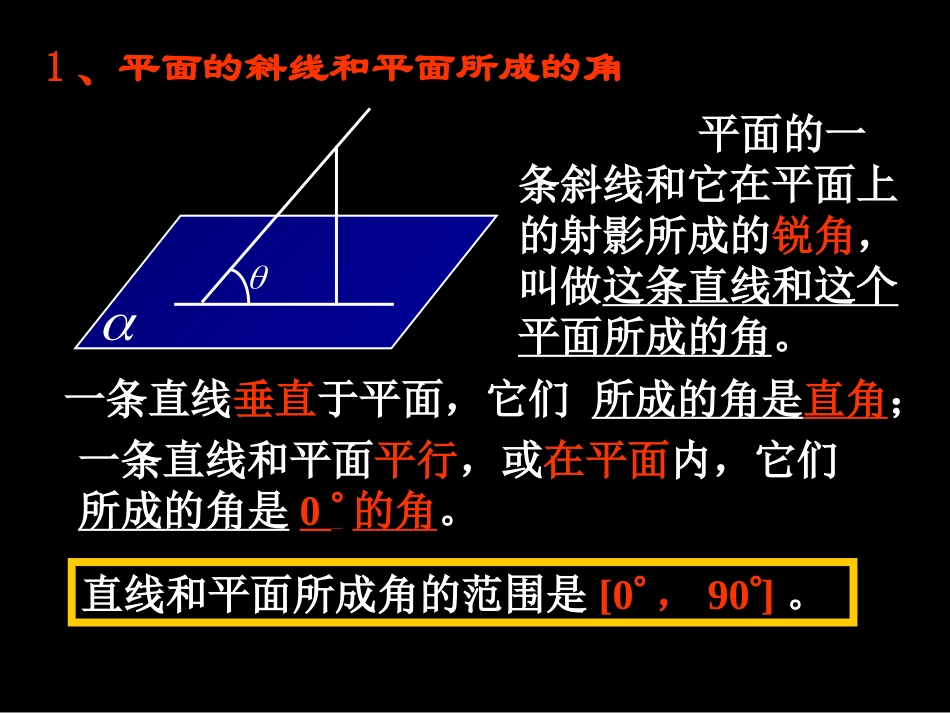
AlBO2、从平面外同一点分别作该平面的垂线段和斜线段：1、点在平面上的射影是一个点，斜线在平面上的射影是一条直线；直线在平面上的射影是一个点或一条直线复习回顾（1）射影相等的两条斜线段相等，射影较长的斜线段也较长；（2）相等的斜线段的射影相等，较长的斜线段的射影也较长；（3）垂线段比任何一条斜线段都短。平面的一条斜线和它在平面上的射影所成的锐角，叫做这条直线和这个这条直线和这个平面所成的角平面所成的角。一条直线垂直于平面，它们所成的角是所成的角是直角直角；一条直线和平面平行，或在平面内，它们所成的角是所成的角是00的角的角。直线和平面所成角的范围是[0[0，，9090]]。1、平面的斜线和平面所成的角AlBOD则则θθ与∠∠AODAOD的大小关系如何？在Rt△AOB和Rt△AOC中sinABAOsinACAODAO∵AB＜AC，∴sinθ＜sin∠AOD∴θ＜∠AOD斜线和平面所成的角，是这条斜线和平面内经过斜足的直线所成的一切角中最小的角。C最小角原理l是平面的斜线，A是l上任意一点，AB是平面的垂线，B是垂足，OB是斜线l的射影,θθ是斜线l与平面所成的角.引例如图，AO是平面π的斜线，OB⊥平面π于B，AD是π内不与AB重合的直线∠OAB=，∠BAD=，∠OAD=，求证：cos=coscosOBADC证明:设|AO|=1则||||coscos,ABAO�||||coscoscos,ACAB�||||cos,OACACAO�在直角中coscoscos.例1ABB已知为平面内的一条射线,为斜足,AO0,,,60,OBCABC为垂足为内的一条射线045,.OBCAB求斜线和平面所成的角ACOB解:由最小角原理得coscoscosABCOBC00cos60cos45cos即00cos602cos.cos452练习1.AO与平面斜交，O为斜足，AO与平面成角，B是A在上的射影,OD是内的直线，∠BOD=30，∠AOD=60，则sin=。BAODC解:由最小角原理得coscoscosAODBOD00cos60cos30cos即3cos363练习2.已知斜线段的长是它在平面β上射影的2倍，则斜线和平面β所成的角______。βABO0603.求证两条平行直线和一个平面所成的角相等.CD,//,ABCDABCD已知:是平面的斜线且,ABCD求证:与平面所成的角相等.证明:,,,ACAOCE过分别作连BO,DE.E∵AB//CD，AO//CE，又∠AOB=∠CED=900∴∠ABO=∠CDE。即两平行直线与平面所成角相等如果两条直线与一个平面所成的角相等，它们平行吗？不一定。例题例例11.如图，在Rt△ABC中，已知∠C=90，AC=BC=1，PA⊥平面ABC，且PA=2，求PB与平面PAC所成的角.PACB解：PA⊥平面ABCPABC⊥平面PAC又ACBCPA⊥∵AC=1,PA=2PC=3平面ABCBC⊥平面PACAC=APB与平面PAC所角为∠BPC又BC=1，tanBPC=∠33∠BPC=30CAPB11即BP与平面PAC所成的角为30.与平面ABCD所成的角例２、如图,在正方体1111DCBAABCD中，与平面A1B1CD所成的角BA1求BCA1ADB1C1D1OAD1与平面ABCD所成角A1B与平面BB1D1D所成角练习4、例例例例例例例例ABCD－A1B1C1D1中，求AD1和平面A1D1CB所成的角。例例例例例AD1在平面A1D1CB内的射影。例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例A1D1C1B1ABCDO112OAAD0130.ADO1.平面的一条斜线和它在平面上的射影所成的锐角，叫做这条直线和这个平面所成的角这条直线和这个平面所成的角。2.最小角原理:斜线和平面所成的角，是这条斜线和平面内任意的直线所成的一切角中最小的角。例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例例小结