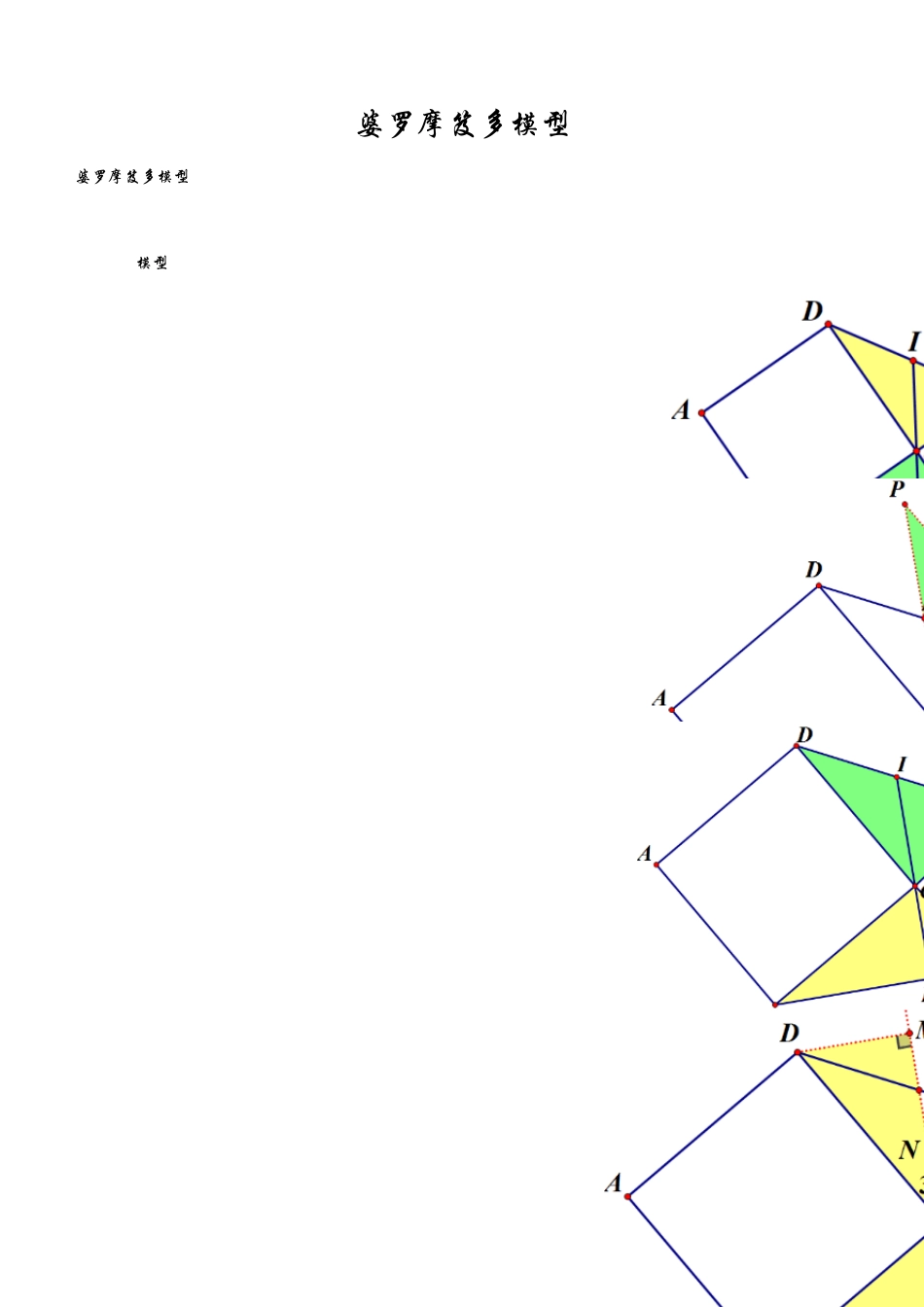
婆罗摩笈多模型婆罗摩笈多模型条件:1)公共顶点:顶点 C2)等线段:BC=DCCE=CG3)顶角相等:∠DCB=∠GCE=90°一、基础模型【问题一 已知中点证垂直】已知:四边形ABCD、CEFG为正方形,连接 BE、DG,I、C、H三点共线若点 I为中点,则 CH⊥ BE,BE=2IC,S∆DCG=S∆BCE证明 (思路):①延长 IC到点 P,使 PI=IC,连接 PG先证明 ∆DIC≌∆GIP(SAS),所以 DC=PG,∠DCI=∠P 则DC‖PG 四边形 ABCD、CEFG为正方形∴DC=BCCE=CG∠GCE=∠BCD=90°∴BC=PG ∠PGC==180°-∠DCG(两直线平行同旁内角互补)∠BCE=360°-90°-90°-∠DCG=180°-∠DCG∴∠PGC=∠BCE则 ∆PCG≌∆BEC(SAS)∴∠PCG=∠CEB ∠PCG+∠ECH=180°-90°=90°∴∠CEB+∠ECH=90°∴∠CHE=90°∴CH⊥ BE② ∆PCG≌∆BEC∴PC=BE∴BE=2IC③ S∆EBC=S∆PCG=S∆PIG+S∆GCI=S∆DIC+S∆GCI=S∆DCG【问题二 已知垂直证中点】已知:四边形ABCD、CEFG为正方形,连接 BE、DG,I、C、H三点共线若 CH⊥ BE, 则点 I为中点,BE=2IC,S∆DCG=S∆BCE证明 (思路):①分别过点D、G作 DM⊥ CI与点 M,NG⊥ CI于点 N ∠2+∠3=90°,∠1+∠2=90°∴∠1=∠3由已知条件可得 ∆CDM≌∆BCH(AAS)∴DM=CHCM=BH同理 ∆GCN≌∆CEH(AAS)∴NG=CHNC=HE∴NG=DM再证明∆DMI≌∆GNI(AAS)∴DI=IGMI=NI则点I为中点② BE=BH+HE=CM+NC=NM+NC+NC=2NI+2NC=2IC③ S∆BHC=S∆DMCS∆GNC=S∆CHE S∆DMI=S∆GNI∴S∆DCG=S∆DCI+S∆GNI+S∆CNG=S∆DMC+S∆GNC=S∆BHC+S∆CHE=S∆BCE二、变形变形一:如图 ∆AOB、∆COD为等腰直角三角形,连接 AC、BD,MN过点O且与 AC交于点N、BD交于点M则有如下结论:1)若点N为中点,则MN⊥ BD,2)若 MN⊥ BD,则点N为中点3)BD=2ON4)S∆BOD=S∆AOC证明(思路):1)延长 MN至点H,使 NH=NO,连接 HC先证明∆ANO≌∆CNH(SAS),所以 AO=HC,∠AON=∠H 则AO‖HC再证明∆HOC≌∆BDO(SAS)∴∠COH=∠ODBHO=BD∴BD=2ON,S∆BOD=S∆AOC ∠COH+∠DOM=90°K∴∠ODB+∠DOM=90°∴∠OMD=90°∴MN⊥ BD2)方法一:构造一线三垂直模型 (与问题二证明方法相同)方法二:在 BD上截取一点P,使 BP=ON,连接 OP先证明∆ANO≌OBP(SAS) ∴∠ANO=∠BPOAN=OPON=BP再证明∆NOC≌∆PDO(SAS)∴NC=OP ON=PD∴BD=2ON,S∆BOD=S∆AOC变形二:如图 ∆AOB、∆COD为等腰直角三角形,连接 AC、BD,MN过点O且与 AC交于点N、BD交于点M则有如下结论:1)若点N为中点,则MN⊥ BD,2)若MN⊥ BD...