任意角弧度制VIP免费

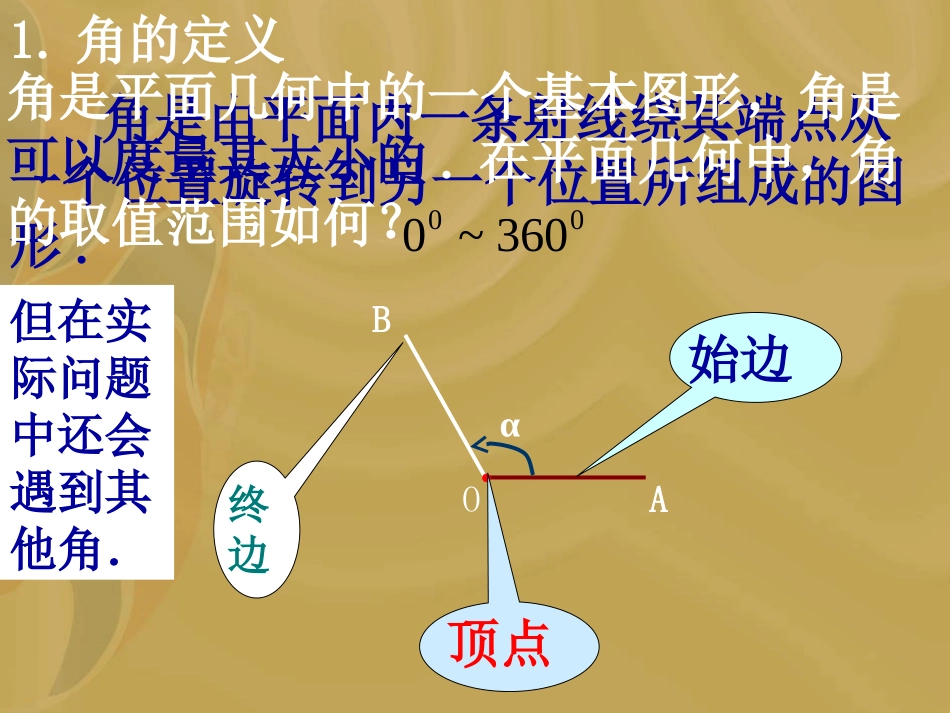
§1.1.1角的概念的推广0AB始边终边顶点角：一条射线绕着它的端点在平面内旋转形成的图形1.角的定义角是由平面内一条射线绕其端点从一个位置旋转到另一个位置所组成的图形.AOBα始边终边顶点角是平面几何中的一个基本图形，角是可以度量其大小的.在平面几何中，角的取值范围如何？00360~0但在实际问题中还会遇到其他角．探究一：角的形成结果；在齿轮传动中，被动轮与主动轮是按相反方向旋转的.一般地，一条射线绕其端点旋转，既可以按逆时针方向旋转，也可以按顺时针方向旋转.你认为将一条射线绕其端点按逆时针方向旋转60度所形成的角，与按顺时针方向旋转60度所形成的角是否相等？如在体操、花样滑冰、跳台跳水等比赛中，常常听到“转体10800”、“转体12600”这样的解说．因此，仅有0°～360°范围内的角是不够的．逆时针顺时针角定义：正角：按逆时针方向旋转形成的角负角：按顺时针方向旋转形成的角零角：射线不做旋转时形成的角任意角•度量一个角的大小，既要考虑旋转方向，又要考虑旋转量，通过以下规定，角的范围就扩展到：任意大小.xyo始边终边终边终边终边1)置角的顶点于原点终边落在第几象限就是第几象限角2)始边重合于X轴的正半轴终边ⅠⅡⅢⅣ如果角的终边在坐标轴上，就认为这个角不属于任何象限，或称这个角为轴线角.那么下列各角：-50°，405°，210°,-200°，－450°分别是第几象限的角？－50°xyoxyo405°xyo210°xyo－200°xyo对于你能用图形表示这些角吗？你能总结一下作图的要点吗？000660,150,210画图表示一个大小一定的角:(1)先画一条射线作为角的始边，(2)再由角的正负确定角的旋转方向，(3)再由角的绝对值大小确定角的旋转量，(4)画出角的终边，并用带箭头的螺旋线加以标注.βB2γAB1αO问题３：第二象限的角一定比第一象限的角大吗？象限角只能反映角的终边所在象限(位置)，不能反映角的大小.问题2：锐角是第几象限的角？第一象限的角是否都是锐角？小于90°的角是锐角吗？xyo3003900-33003900=300+3600－3300=300－3600=300+1x3600=300－1x3600300==300+0x3600300+2x3600,300－2x3600300+3x3600,300－3x3600…,…,与300终边相同的角的一般形式为300＋K·3600,K∈Z与ａ终边相同的角的一般形式为ａ＋K·3600，K∈ZS={β|β=a+K·3600,K∈Z}探究三：终边相同的角例2写出终边落在坐标轴上的角的集合。终边落在坐标轴上的情形xyo0090018002700+Kx3600+Kx3600+Kx3600+Kx3600或3600＋KX3600129°48′，第二象限角.300°，-60°.例题分析例1．在0°～360°范围内，找出与－950°12′角终边相同的角，并判定它是第几象限角.例2．求与3900°终边相同的最小正角和最大负角.例题示范A.终边相同的角一定相等B.第一象限的角都是锐角C.锐角都是第一象限的角D.小于90°的角都是锐角例1(1)下列各命题正确的是例题示范例2(2)下列各对角中，终边相同的是580280.和A485125.和B0360.和C36412.和D例题示范例4(1)与405°角终边相同的角是)(457360.ZkkA)(405360.ZkkB)(45360.ZkkC)(45180.ZkkD例题示范例4(2)终边与坐标轴重合的角的集合是ZkkA,360|.ZkkB,180|.ZkkC,90|.ZkkD,90180|.例题示范例5写出终边落在阴影部分(含边界)的角的集合例题示范例6已知α=1690°,(1)把α改写k·360°+β(kZ,0°≤β<360°)∈的形式;(2)求θ,使θ与α的终边相同,且-360°<θ<360°,并且判定θ属于第几象限?;3604250)1(,3601690)2(k250,110,)360,360(中其中在是第三象限角•解:终边在终边在射线y=x上的角的集合是终边在终边在射线y=-x上的角的集合是所以终边在y=x上的角的集合是B={α/α=225°+k×360°,kZ}∈A={α/α=45°+k×360°,kZ}∈S={α/α=225°+k×360°,kZ}∈∪{α/α=45°+k×360°,kZ}∈={α/α=45°+k×180°,kZ}∈例3:写出终边在直线y=x上的角的集合S,并把S中适合不等式-360°≤β＜720°的元素β写出来Ｓ中适合-360°≤β＜720°的元素45°－2x180...