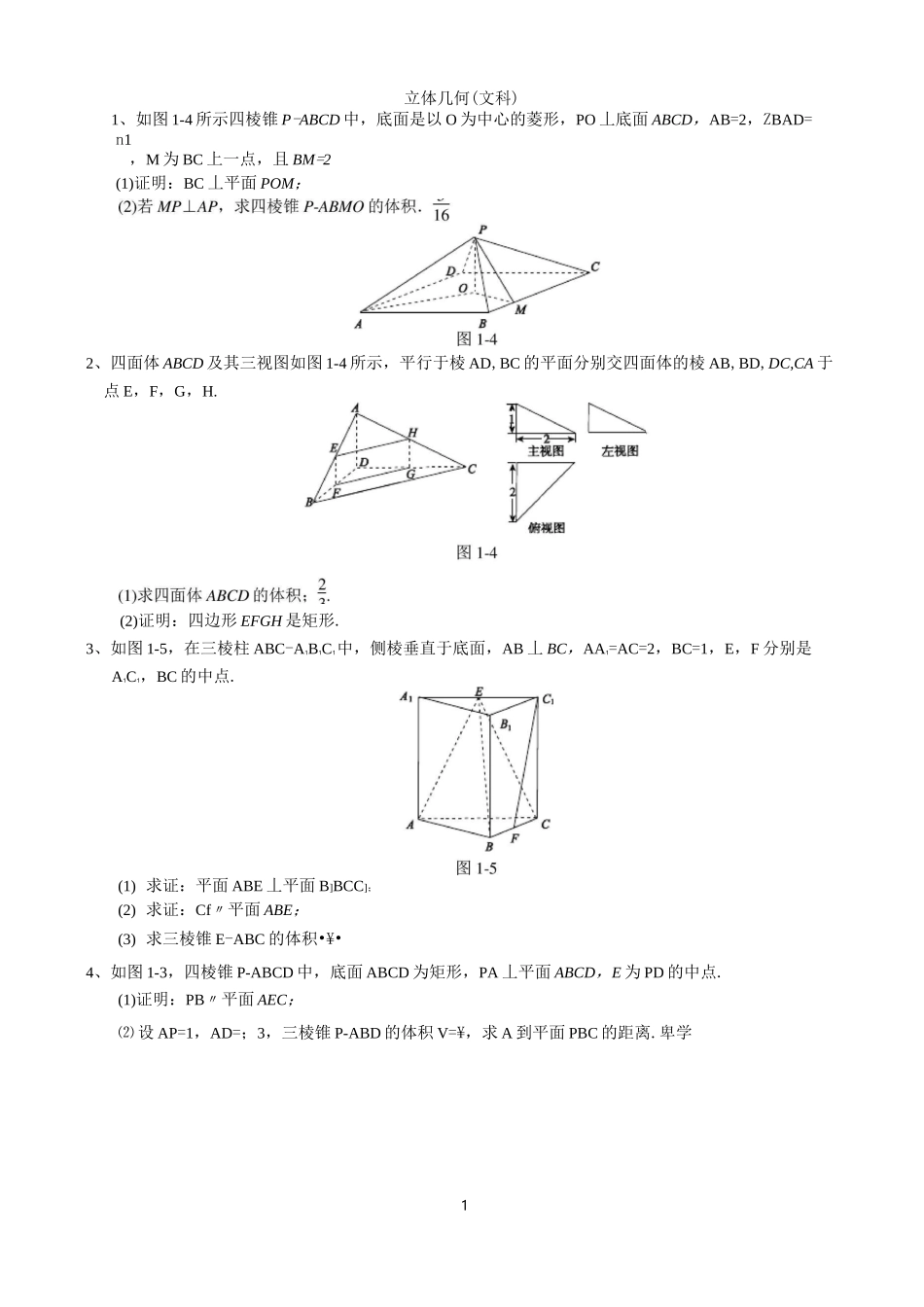
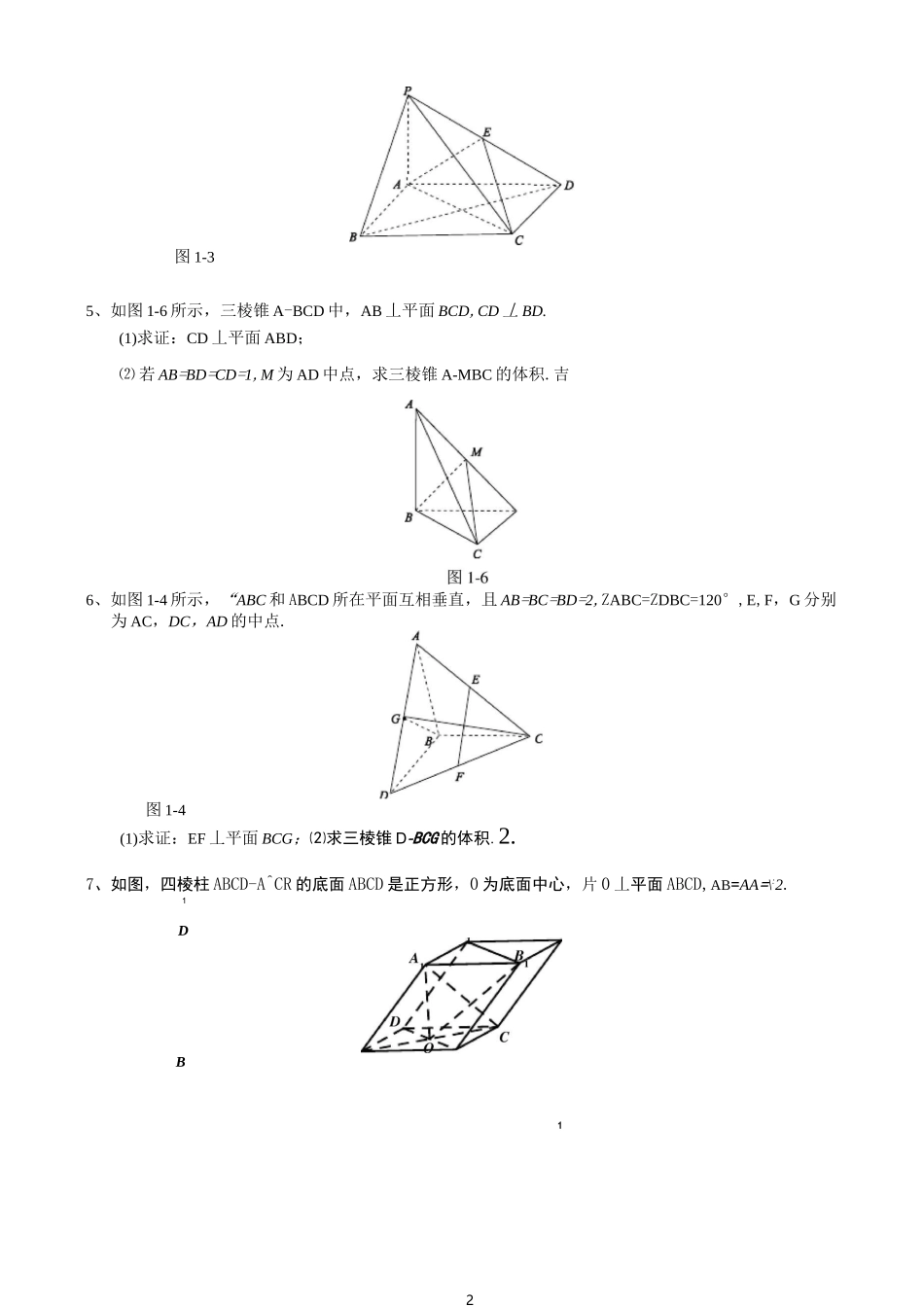
1立体几何(文科)1、如图 1-4 所示四棱锥 P-ABCD 中,底面是以 O 为中心的菱形,PO 丄底面 ABCD,AB=2,ZBAD=n1,M 为 BC 上一点,且 BM=2(1)证明:BC 丄平面 POM;2、四面体 ABCD 及其三视图如图 1-4 所示,平行于棱 AD,BC 的平面分别交四面体的棱 AB,BD,DC,CA 于点 E,F,G,H.(2)证明:四边形 EFGH 是矩形.3、如图 1-5,在三棱柱 ABC-A1B1C1中,侧棱垂直于底面,AB 丄 BC,AA1=AC=2,BC=1,E,F 分别是A1C1,BC 的中点.(1) 求证:平面 ABE 丄平面 B]BCC];(2) 求证:Cf〃平面 ABE;(3) 求三棱锥 E-ABC 的体积•¥•4、如图 1-3,四棱锥 P-ABCD 中,底面 ABCD 为矩形,PA 丄平面 ABCD,E 为 PD 的中点.(1)证明:PB〃平面 AEC;⑵ 设 AP=1,AD=;3,三棱锥 P-ABD 的体积 V=¥,求 A 到平面 PBC 的距离.卑学12图 1-35、如图 1-6 所示,三棱锥 A-BCD 中,AB 丄平面 BCD,CD 丄 BD.(1)求证:CD 丄平面 ABD;⑵ 若 AB=BD=CD=1,M 为 AD 中点,求三棱锥 A-MBC 的体积.吉6、如图 1-4 所示,“ABC 和 ABCD 所在平面互相垂直,且 AB=BC=BD=2,ZABC=ZDBC=120°,E,F,G 分别为 AC,DC,AD 的中点.图 1-4(1)求证:EF 丄平面 BCG;⑵求三棱锥 D-BCG 的体积.2.7、如图,四棱柱 ABCD-A^CR 的底面 ABCD 是正方形,0 为底面中心,片 0 丄平面 ABCD,AB=AA=\:2.1DB3(I)证明:ABD//平面 CDB;(II) 求三棱柱 ABD-A1B1D1的体积.&如图,在四棱锥 P-ABCD中,PD 丄面 ABCD,ABIIDC,AB 丄 AD,BC=5,DC=3,AD 二 4,ZPAD 二 60。.(1) 当正视图方向与向量 AD 的方向相同时,画出四棱锥 P-ABCD 的正视图•(要求标出尺寸,并画出演算过程);(2) 若 M 为 PA 的中点,求证:DM//面 PBC;⑶ 求三棱锥 D-PBC 的体积.9、如图 4,在边长为 1 的等边三角形 ABC 中,D,E 分别是 AB,AC 边上的点,AD=AE,F 是 BC 的中点,AF 与 DE 交于点 G,将 AABF 沿 AF 折起,得到如图 5 所示的三棱锥 A-BCF,其中(1)证明:DE//平面 BCF;证明:CF 丄平面 ABF;213F-DEG4当 AD=-时,求三棱锥 F-DEG 的体积 V图5=1.1.DG-FG-GF=1-1-1•1.迈.1=二/3F—DEGE—DFG323233233243324111如图,三棱柱 ABC—ABC 中,CA=CB,AB 二 AA,ZBAA=60。.11111(I)证明:AB 丄 AC;(H)若 AB=CB=2,ACf 虽,求三棱柱 ABC—ABC 的体积.因为 OC^AB 二 O,所以 OA 丄平面...