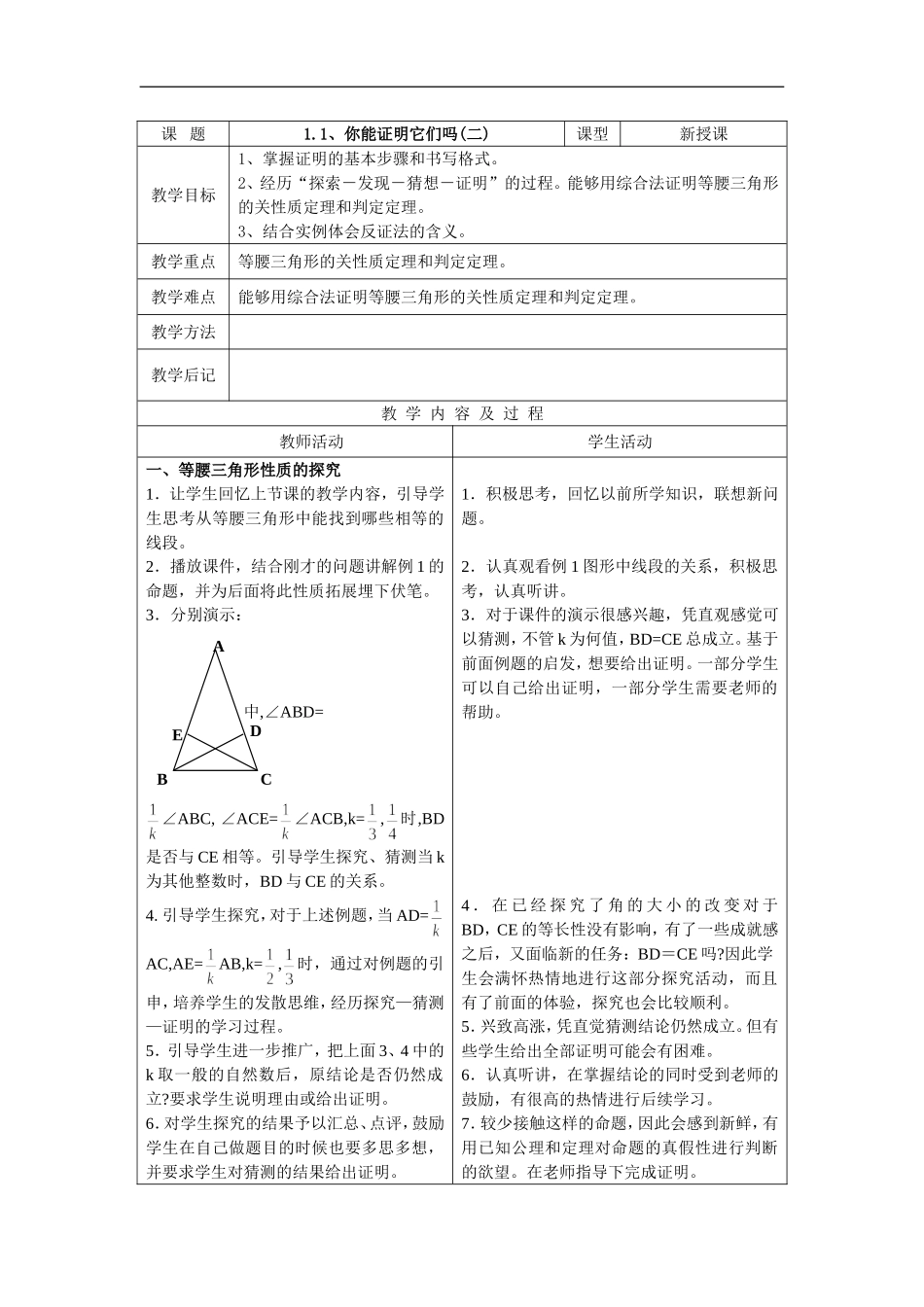
课 题1.1、你能证明它们吗(二)课型新授课教学目标1、掌握证明的基本步骤和书写格式。2、经历“探索-发现-猜想-证明”的过程。能够用综合法证明等腰三角形的关性质定理和判定定理。3、结合实例体会反证法的含义。教学重点等腰三角形的关性质定理和判定定理。教学难点能够用综合法证明等腰三角形的关性质定理和判定定理。教学方法教学后记教 学 内 容 及 过 程教师活动学生活动一、等腰三角形性质的探究1.让学生回忆上节课的教学内容,引导学生思考从等腰三角形中能找到哪些相等的线段。2.播放课件,结合刚才的问题讲解例 1 的命题,并为后面将此性质拓展埋下伏笔。3.分别演示: 中,∠ABD= ∠ABC, ∠ACE=∠ACB,k=,时,BD是否与 CE 相等。引导学生探究、猜测当 k为其他整数时,BD 与 CE 的关系。4. 引导学生探究,对于上述例题,当 AD=AC,AE=AB,k=,时,通过对例题的引申,培养学生的发散思维,经历探究—猜测—证明的学习过程。5.引导学生进一步推广,把上面 3、4 中的k 取一般的自然数后,原结论是否仍然成立?要求学生说明理由或给出证明。6.对学生探究的结果予以汇总、点评,鼓励学生在自己做题目的时候也要多思多想,并要求学生对猜测的结果给出证明。1.积极思考,回忆以前所学知识,联想新问题。2.认真观看例 1 图形中线段的关系,积极思考,认真听讲。3.对于课件的演示很感兴趣,凭直观感觉可以猜测,不管 k 为何值,BD=CE 总成立。基于前面例题的启发,想要给出证明。一部分学生可以自己给出证明,一部分学生需要老师的帮助。4 . 在 已 经 探 究 了 角 的 大 小 的 改 变 对 于BD,CE 的等长性没有影响,有了一些成就感之后,又面临新的任务:BD=CE 吗?因此学生会满怀热情地进行这部分探究活动,而且有了前面的体验,探究也会比较顺利。5.兴致高涨,凭直觉猜测结论仍然成立。但有些学生给出全部证明可能会有困难。6.认真听讲,在掌握结论的同时受到老师的鼓励,有很高的热情进行后续学习。7.较少接触这样的命题,因此会感到新鲜,有用已知公理和定理对命题的真假性进行判断的欲望。在老师指导下完成证明。ABCDE7.提出新的问题,引导学生从“等角对等边”这个命题的反面思考问题,即思考它的逆命题是否成立。适时地引导学生思考可以用哪些方法证明?培养学生的推理能力。8.归纳学生提出的各种证法,清楚的分析证明的思路,培养学生演绎证明的初步的推理能力。9.启发学生思考:在...