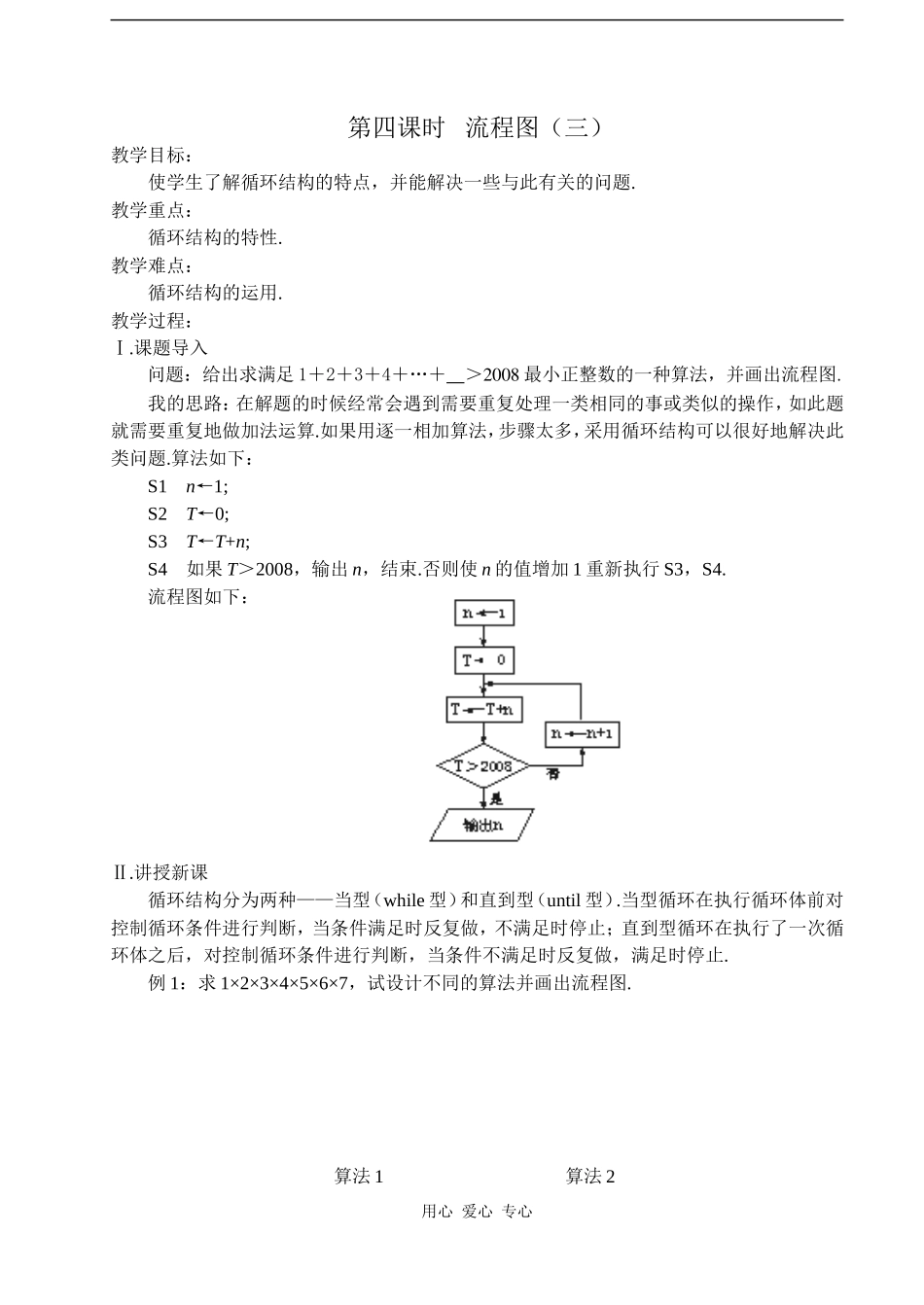
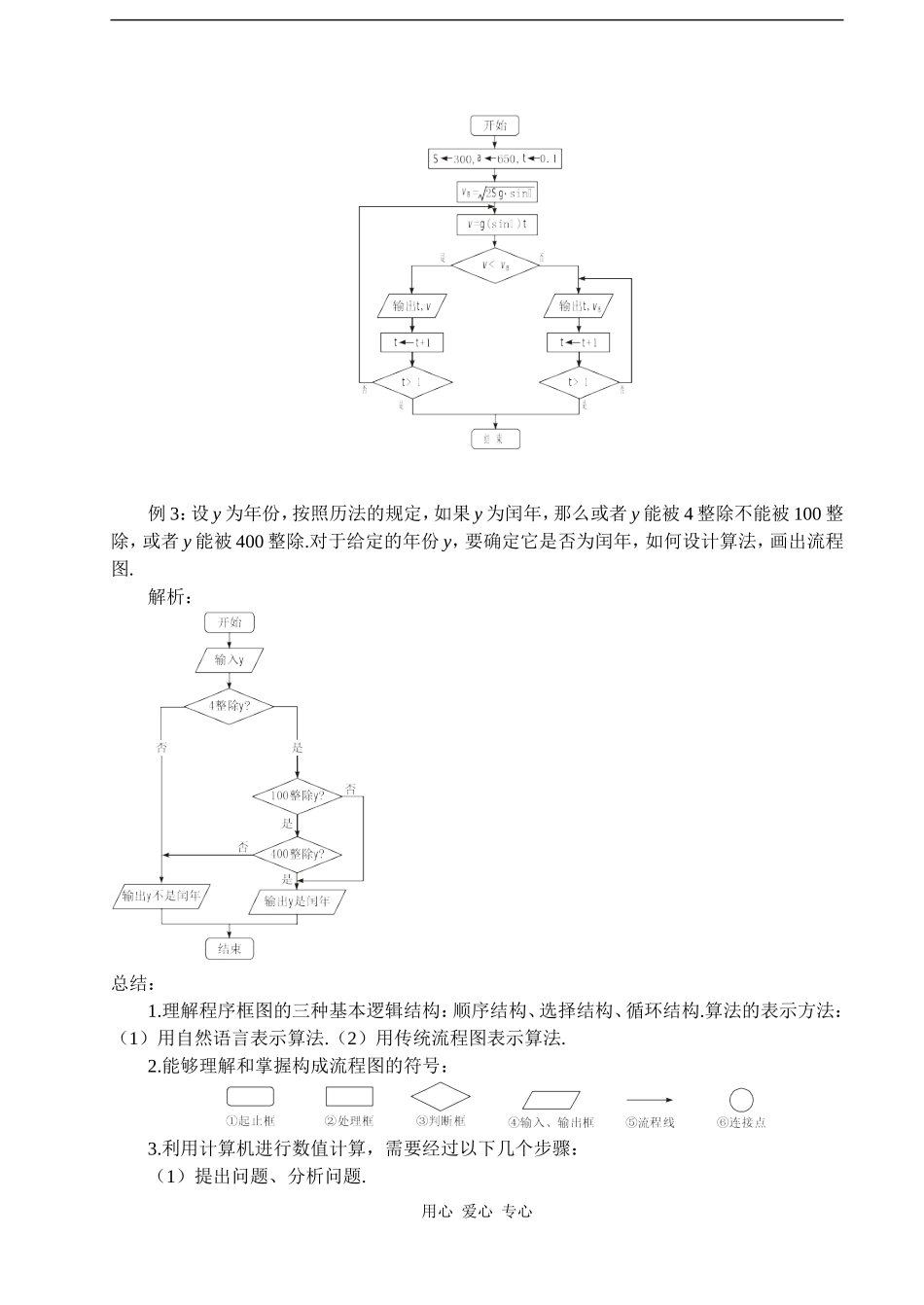
第四课时 流程图(三)教学目标:使学生了解循环结构的特点,并能解决一些与此有关的问题.教学重点:循环结构的特性.教学难点:循环结构的运用.教学过程:Ⅰ.课题导入问题:给出求满足 1+2+3+4+…+ >2008 最小正整数的一种算法,并画出流程图.我的思路:在解题的时候经常会遇到需要重复处理一类相同的事或类似的操作,如此题就需要重复地做加法运算.如果用逐一相加算法,步骤太多,采用循环结构可以很好地解决此类问题.算法如下:S1 n←1;S2 T←0;S3 T←T+n;S4 如果 T>2008,输出 n,结束.否则使 n 的值增加 1 重新执行 S3,S4.流程图如下:Ⅱ.讲授新课循环结构分为两种——当型(while 型)和直到型(until 型).当型循环在执行循环体前对控制循环条件进行判断,当条件满足时反复做,不满足时停止;直到型循环在执行了一次循环体之后,对控制循环条件进行判断,当条件不满足时反复做,满足时停止.例 1:求 1×2×3×4×5×6×7,试设计不同的算法并画出流程图.算法 1 算法 2用心 爱心 专心 点评:本题主要考查学生对顺序结构和循环结构的理解,学会推理分析.算法都可以由顺序结构、选择结构和循环结构这三块“积木”通过组合和嵌套来完成.算法 2 具有通用性、简明性.流程图可以帮助我们更方便直观地表示这三种基本的算法结构. 例 2:有一光滑斜面与水平桌面成 α 角,设有一质点在 t=0 时,从此斜面的顶点 A 处开始由静止状态自由释放,如下图所示.如果忽略摩擦力,斜面的长度 S=300 cm,α=65°.求 t=0.1,0.2,0.3,…,1.0 s 时质点的速度.试画出流程图.解析:从物理学知识知道:质点在斜面上运动时,它的加速度 a=gsinα.当在水平面上运动时,速度为常数,且保持它在 B 点时的速度.从 A 点到 B 点间的速度 v,可由公式 v=at=g(sinα)t 求出,到 B 点时的速度 vB为vB=at=a==2Sg·sinα.解题的过程是这样考虑的:按公式 v=at=g(sinα)t,求 t=0.1,0.2,0.3……时的速度 v,每求出对应于一个 t 的 v 值后,即将 v 与 vB相比较,如果 v<vB,表示质点还未到达 B 点,使 t 再增加 0.1 s,再求下一个 t时的 v 值,直到 v≥vB时,此时表示已越过 B 点,此后的速度始终等于 vB的值.流程图如下:用心 爱心 专心例 3:设 y 为年份,按照历法的规定,如果 y 为闰年,那么或者 y 能被 4 整除不能被 100 整除,或者 y 能被 400 整...